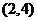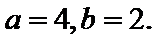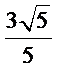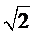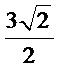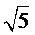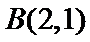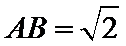- 一元二次不等式的解法
- 共69题
1
题型:填空题
|
1. 设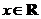
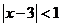
正确答案
知识点
一元二次不等式的解法
1
题型:
单选题
|
2.设变量


正确答案
C
解析
作出不等式组对应的平面区域如图:(阴影部分).由z=3x+y得y=-3x+z,平移直线y=-3x+z,由图象可知当直线y=-3x+z经过点A时,直线y=-3x+z的截距最大,此时z最大.,当 
考查方向
本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.
解题思路
线性规划也是高考中常考的知识点,一般以客观题形式出现,基本题型是给出约束条件求目标函数的最值,常见的结合方式有:纵截距、斜率、两点间的距离、点到直线的距离,解决此类问题常利用数形结合,准确作出图形是解决问题的关键
易错点
根据题意正确作出约束条件对应的平面区域图象.
知识点
一元二次不等式的解法
1
题型:填空题
|
12.已知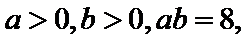
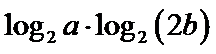
正确答案
4
解析
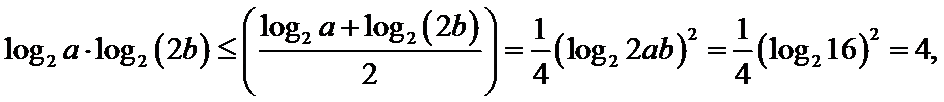
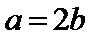
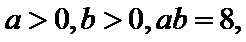
考查方向
本题主要考查对数运算法则及基本不等式应用
解题思路
在利用基本不等式求最值时,一定要紧扣“一正、二定、三相等”这三个条件,注意创造“定”这个条件时常要对所给式子进行拆分、组合、添加系数等处理,使之可用基本不等式来解决,若多次使用基本不等式,必须保持每次取等的一致性.
易错点
不等式取等号的条件
知识点
一元二次不等式的解法
1
题型:
单选题
|
4. 若平面区域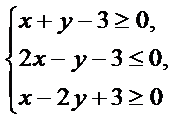
正确答案
B
解析
画出不等式组的平面区域如题所示,由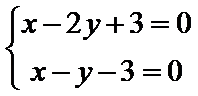
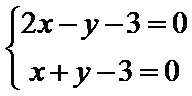
由题意知,当斜率为1的两条直线分别过点A和点B时,两直线的距离最小,即
考查方向
本题主要考查了线性规划.等知识,为高考题的必考题,在近几年的各省高考题出现的频率较高
解题思路
画出可行域,利用垂直性质和两点间距离公式求出
易错点
对可行性区域的划分出现错误
知识点
一元二次不等式的解法
1
题型:填空题
|
5.函数
正确答案

解析



考查方向
函数定义域
解题思路
列出满足要求的不等式,利用不等式求解
易错点
列出所有满足要求的不等式
知识点
函数的定义域及其求法一元二次不等式的解法
下一知识点 : 不等式恒成立问题
扫码查看完整答案与解析