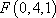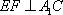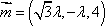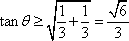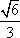- 抛物线的标准方程和几何性质
- 共238题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
在




(1)a和c的值;
(2)
正确答案
(1)a=3,c=2
(2)
解析
(1)∵


∴c•acosB=2,即ac=6①,
∵b=3,
∴由余弦定理得:b2=a2+c2﹣2accosB,即9=a2+c2﹣4,
∴a2+c2=13②,
联立①②得:a=3,c=2;
(2)在△ABC中,sinB=


由正弦定理





∵a=b>c,∴C为锐角,
∴cosC=


则cos(B﹣C)=cosBcosC+sinBsinC=




知识点
叙述并证明余弦定理。
正确答案
见解析
解析
叙述:
余弦定理:三角形任何一边的平方等于其他两遍平方的和减去这两边与它们夹角的余弦之积的两倍。或:在△ABC中,a,b,c为A,B,C的对边,有



证明:(证法一) 如图,
即
同理可证 
(证法二)已知






∴

即
同理可证 
知识点
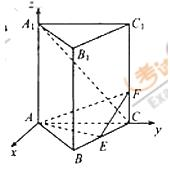
如图,已知正三棱柱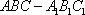
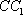
(1)当CF=1时,求证: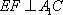
(2)设二面角C-AF-E的大小为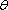
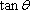
正确答案
见解析
解析
(1)建立如图所示的空间直角坐标系,则有已知可得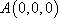
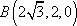

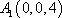
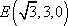
于是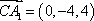
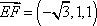
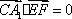
(2)设

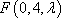
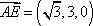
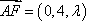

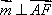
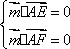
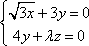
又由直三棱柱的性质可取侧面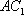
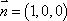
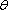
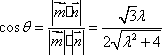
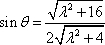
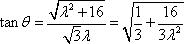
由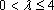

故当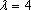

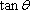
知识点
设






正确答案
解析



即


知识点
扫码查看完整答案与解析