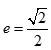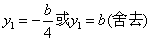- 抛物线的标准方程和几何性质
- 共238题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知集合M={1,2,3},N={2,3,4},则
正确答案
解析
本题考查了集合的交、并、补运算.∵

知识点
在某种信息传输过程中,用4个数字的一个排列(数字允许重复)表示一个信息,不同排列表示不同信息,若所用数字只有0和1,则与信息0110至多有两个对应位置上的数字相同的信息个数为
正确答案
解析
本题考查了排列组合知识.至多有两位上的数字相同,其对立面为三位或者四位上的数字相同,结果为
知识点
已知三点O(0,0),A(-2,1),B(2,1),曲线C上任意一点M(x,y)满足
(1)求曲线C的方程;
(2)动点Q(x0,y0)(-2<x0<2)在曲线C上,曲线C在点Q处的切线为l,问:是否存在定点P(0,t)(t<0),使得l与PA,PB都相交,交点分别为D,E,且△QAB与△PDE的面积之比是常数?若存在,求t的值;若不存在,说明理由。
正确答案
见解析
解析
(1)由

得

由已知得
化简得曲线C的方程:x2=4y.
(2)假设存在点P(0,t)(t<0)满足条件,
则直线PA的方程是
曲线C在点Q处的切线l的方程是

由于-2<x0<2,因此-1<
①当-1<t<0时,

②当t≤-1时,

所以l与直线PA,PB一定相交。
分别联立方程组
解得D,E的横坐标分别是

则xE-xD=(1-t)
又|FP|=-


又
于是
=
对任意x0∈(-2,2),要使
解得t=-1.此时
故存在t=-1,使得△QAB与△PDE的面积之比是常数2.
知识点
已知f(x)是定义在R上的偶函数,且以2为周期,则“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的( )
正确答案
解析
由题意,f(x)是定义在R上的偶函数,f(x)为[0,1]上的增函数
所以f(x)为[﹣1,0]上是减函数
又f(x)是定义在R上的函数,且以2为周期[3,4]与[﹣1,0]相差两个周期,故两区间上的单调性一致,所以可以得出f(x)为[3,4]上的减函数,故充分性成立,若f(x)为[3,4]上的减函数,由周期性可得出f(x)为[﹣1,0]上是减函数,再由函数是偶函数可得出f(x)为[0,1]上的增函数,故必要性成立
综上,“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的充要条件。
知识点
将参加夏令营的600名学生编号为:001,002,……600,采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003,这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495住在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数一次为
正确答案
解析
依题意可知,在随机抽样中,首次抽到003号,以后每隔12个号抽到一个人,则分别是003、015、027、039
知识点
设椭圆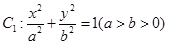
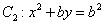
(1)若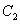
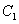
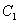
(2)设A(0,b),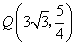
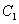
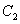
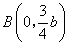
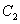
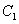
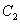
正确答案
(1)
解析
(1)由已知椭圆焦点(c,0)在抛物线上,可得: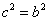
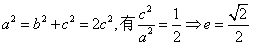
(2)由题设可知M、N关于y轴对称,设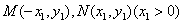
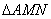
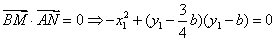
由点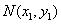
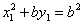
故
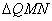

由重心在抛物线上得: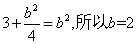
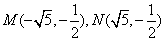
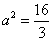
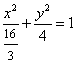
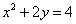
知识点
以抛物线
正确答案
解析
因为已知抛物线的焦点坐标为(1,0),即所求圆的圆心,又圆过原点,所以圆的半径为

知识点
已知定义域为





①对任意









其中所有正确结论的序号是 。
正确答案
①②④
解析
1











知识点
已知等差数列





(1)求数列
(2)令




正确答案
见解析。
解析
(1)
解得
(2)
知识点
扫码查看完整答案与解析