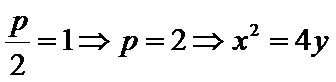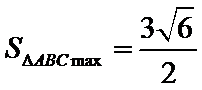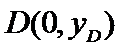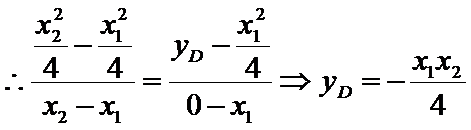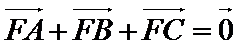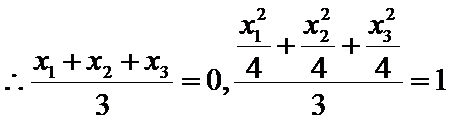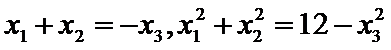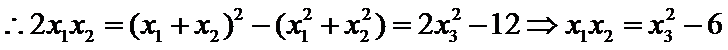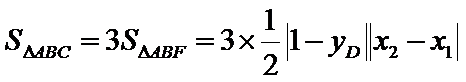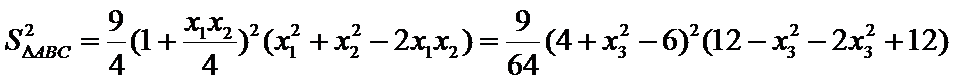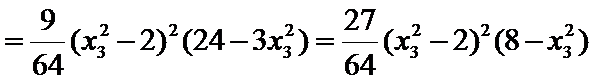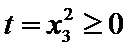- 抛物线的标准方程和几何性质
- 共238题
已知抛物线









23.求
24.若圆




正确答案
(1)抛物线

解析
试题分析: 本题属于抛物线、直线、圆的方程及位置关系考查题型,意在考查考生的分析问题、解决问题的能力及运算能力。
(Ⅰ)设

又∵以


∴




考查方向
解题思路
(1)直线








(2)通过直线

易错点
以


正确答案
(2)直线

圆
解析
试题分析: 本题属于抛物线、直线、圆的方程及位置关系考查题型,意在考查考生的分析问题、解决问题的能力及运算能力。
(Ⅱ)设直线


化简整理得
∴


∴圆心

∵圆


∴
∴

此时直线


圆心

圆

考查方向
解题思路
(1)直线








(2)通过直线

易错点
以


11.已知





正确答案
解析
由题意知,










考查方向
解题思路
1.先根据题意构造函数

易错点
1.不会构建函数

知识点
14. 已知直线l:y=kx+t号圆:x2 +(y+l)2 =1相切且与抛物线C:x2 =4y交于不同的两点M,N,则实数t的取值范围是____.
正确答案
解析
因为直线与圆相切





考查方向
解题思路
先利用直线与圆相切找到k与t之间的关系,再通过直线与抛物线有两个不同的交点求出t的取值范围。
易错点
直线中有两个变量,如何把k转化或者求出。
知识点
已知点F(0,1)为抛物线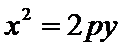
24.求抛物线C的方程;
25.点A、B、C是抛物线上三点且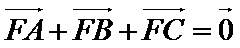
正确答案
(1)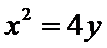
解析
(1)由题意知
考查方向
解题思路
1)第一问利用抛物线的定义,可求出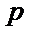
2)第二问首先设出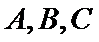
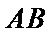
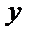
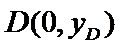
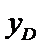
易错点
错位相减法求和计算容易错。
正确答案
(2)
解析
(2)令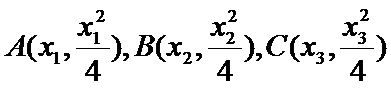
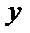
又因为
从而
令
当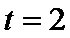
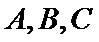
当
考查方向
解题思路
1)第一问利用抛物线的定义,可求出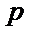
2)第二问首先设出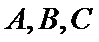
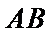
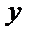
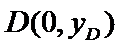
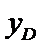
易错点
错位相减法求和计算容易错。
已知抛物线












24.求点

25.已知点








26.已知

















正确答案
(1)
解析
(1)由题意
所以点


考查方向
解题思路
1根据题意直接求出“特征直线”

易错点
1.不理解特征直线的定义导致无法入手;2.证明充要条件时不知道应该证明充分性和必要性。
正确答案
(1)
解析
设点

所以
线段
所以



因为

考查方向
解题思路
线根据渐近线方程求出
易错点
1.不理解特征直线的定义导致无法入手;2.证明充要条件时不知道应该证明充分性和必要性。
正确答案
见解析
解析
(3)设





解





得
必要性:因为点

当


当


所以
① 充分性:由

当


当


所以点

综上,点

考查方向
解题思路
先证明结论的充分性,后证明其必要性。
易错点
1.不理解特征直线的定义导致无法入手;2.证明充要条件时不知道应该证明充分性和必要性。
扫码查看完整答案与解析