- 抛物线的标准方程和几何性质
- 共238题
已知抛物线x2=4y上一点P到焦点F的距离是5,则点P的横坐标是 。
正确答案
±4
解析
根据抛物线的定义可知P到焦点的距离为5,则其到准线距离也为5。
又∵抛物线的准线为y=﹣1,
∴P点的纵坐标为5﹣1=4。
将y=4 代入抛物线方程得:4×4=x2,解得x=±4
故答案为:±4。
知识点
已知点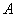
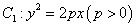
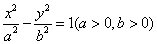
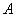
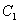
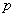
正确答案
解析
略
知识点
曲线









正确答案
解析
略
知识点
在平面直角坐标系xOy中,抛物线C的焦点在y轴上,且抛物线上的点P(x0,4)到焦点F的距离为5,斜率为2的直线l与抛物线C交于A,B两点。
(1)求抛物线C的标准方程,及抛物线在P点处的切线方程;
(2)若AB的垂直平分线分别交y轴和抛物线于M,N两点(M,N位于直线l两侧),当四边形AMBN为菱形时,求直线l的方程。
正确答案
(1)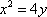
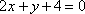
(2)
解析
(1)依题意设抛物线C: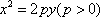
因为点P到焦点F的距离为5,
所以点P到准线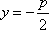
因为P(x0,4),所以由抛物线准线方程可得 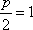
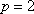
所以抛物线的标准方程为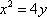
即 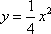
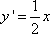
所以 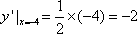
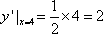
所以 点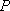
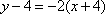
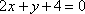
点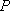
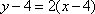
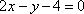
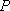
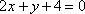
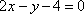
(2)设直线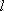
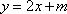
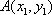
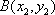
联立 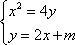
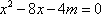
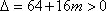
所以 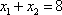
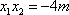
所以 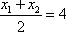
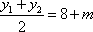
即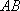
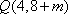
所以 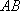
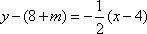
因为 四边形AMBN为菱形,
所以 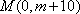
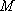
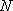
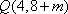
所以 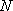
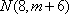
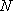
所以 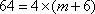
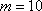
所
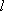
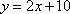
知识点
如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为
(1)求圆M和抛物线C的方程;
(2)设G,H是抛物线C上异于原点O的两个不同点,且
(3)在抛物线C上是否存在两点P,Q关于直线m:y=k(x﹣1)(k≠0)对称?若存在,求出直线m的方程,若不存在,说明理由。
正确答案
见解析。
解析
(1)∵
∴所求抛物线的方程为y2=4x
∴设圆的半径为r,则
(2)设G(x1,y1),H(x2,y2),由

∵

∴x1x2=16,
∵

∴








=

≥


=256
∴
∴△GOH面积最小值为16.
(3)设P(x3,y3),Q(x4,y4)关于直线m对称,且PQ中点D(x0,y0)
∵P(x3,y3),Q(x4,y4)在抛物线C上,
∴

两式相减得:(y3﹣y4)(y3+y4)=4(x3﹣x4)
∴y3+y4=4•

∴y0=﹣2k
∵D(x0,y0)在m:y=k(x﹣1)(k≠0)上
∴x0=﹣1<0,点D(x0,y0)在抛物线外
∴在抛物线C上不存在两点P,Q关于直线m对称
知识点
扫码查看完整答案与解析