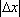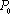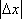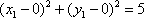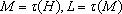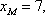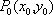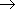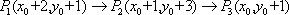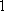- 两点间距离公式的应用
- 共10题
设D为不等式组
正确答案
解析
区域D表示的平面部分如图阴影所示:
根据数形结合知(1,0)到D的距离最小值为(1,0)到直线2x-y=0的距离
知识点
规定函数

①函数
②函数
③若函数


以上命题是真命题的是:
正确答案
解析
知识点
已知点





正确答案
解析
略
知识点
设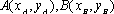
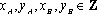
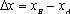
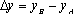
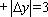
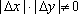
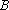
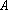
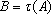
(1)请问:点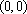
(2)已知点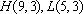
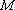
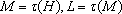
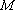
(3)已知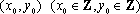
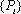
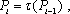
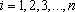
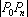
正确答案
见解析
解析
(1)因为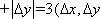
故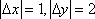
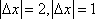
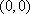

所以这些可能值对应的点在以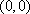

(2)设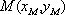
所以有
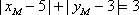
所以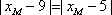
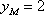
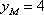
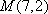
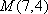
(3)当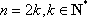
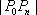
当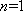
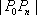

当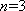

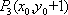
故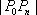
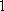
当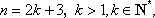

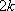
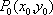
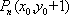
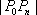
综上,当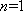
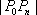
当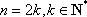
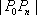
当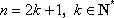
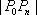
知识点
14.如果











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析