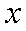- 幂函数的图像
- 共175题
已知函数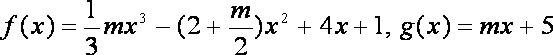
(1)当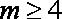

(2)是否存在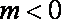
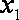


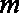
正确答案
见解析
解析
解析:(1)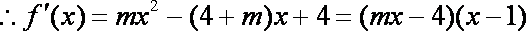
i)若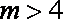
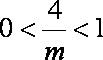

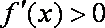
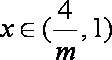
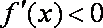
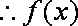
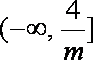
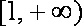
ii)若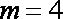
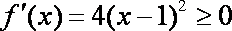
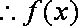
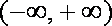
(2)当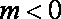
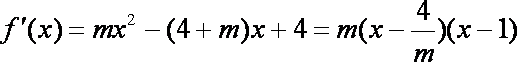
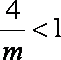
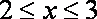

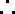
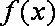
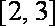
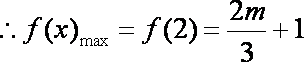
又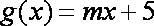
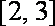
由已知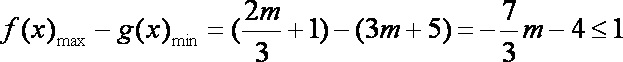
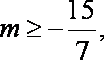

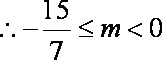
综上所述,存在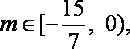
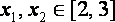
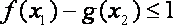
知识点
已知实数


正确答案
解析
略
知识点
已知



(1)求直线

(2)直线



正确答案
见解析
解析
解析:(1)由


所以,


设

∴

∴A(


直线

(2)连结
由椭圆的对称性可知,
所以
又由


知识点
已知函数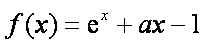
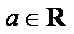
(1)求函数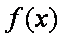
(2)当
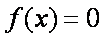
(3)若对任意的
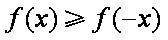
正确答案
见解析
解析
(1)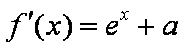
当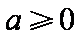
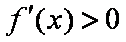
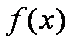
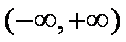
当
由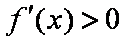
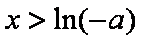
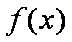
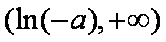
由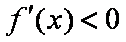
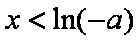

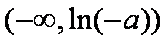
综上,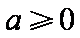
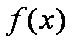
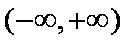
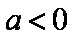
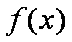
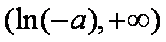
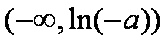
(2)由(1)知,当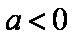
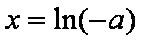
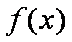
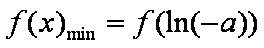
由方程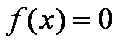
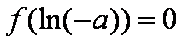

所以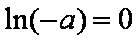
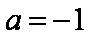
(3)当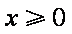
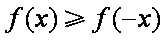
即得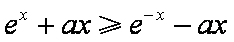

令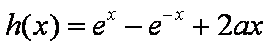
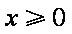
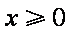
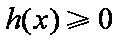
又
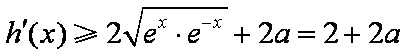
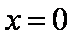
①当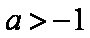
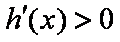
所以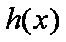
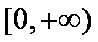
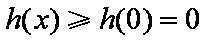
②当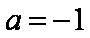
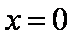
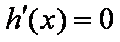
若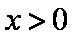
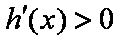
所以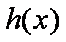
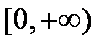
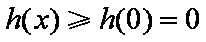
③当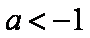


此时,若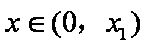
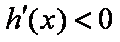

所以,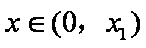
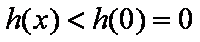
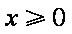
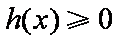
综上,满足条件的
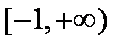
知识点
7.如图所示,使用模拟方法估计圆周率值的程序框图,P表示估计的结果,则图中空白框内应填入P=( )
正确答案
解析
略
知识点
A、B、C三点在同一球面上,

则此球O的体积为
正确答案
解析
略
知识点
已知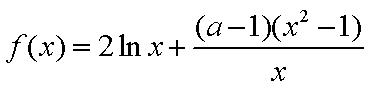
(1)当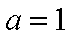
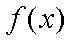
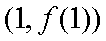
(2)若

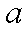
正确答案
(1)2x-y-2=0
(2)(-∞,0]
解析
(1)当
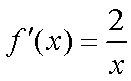
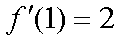
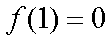
∴所求切线方程为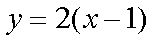
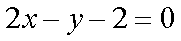
(2)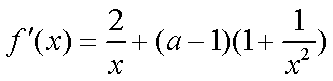
①当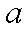
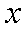
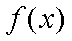
②当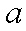
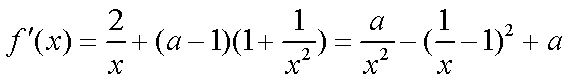
∴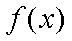

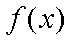
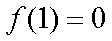
③当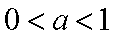
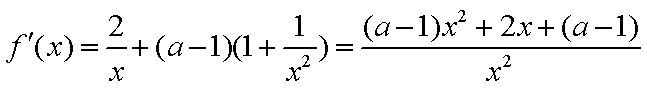
设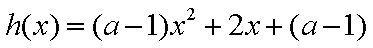
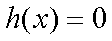
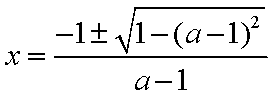
可验证得: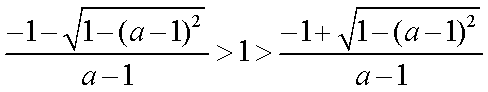
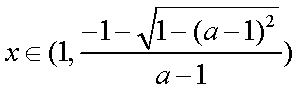
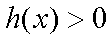
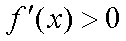
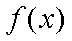
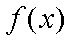
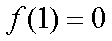
综上实数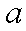
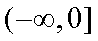
知识点
某工厂的固定成本为





假定该产品产销平衡,根据上述统计规律求:
(1)要使工厂有盈利,产品数量
(2)工厂生产多少台产品时盈利最大?
正确答案
见解析
解析
依题意得


所以
(1)要使工厂有盈利,则有f(x)>0,因为
f(x)>0⇔
⇒
⇒

即
所以要使工厂盈利,产品数量应控制在大于300台小于1050台的范围内, 8分
(2)当
故当x=6时,f(x)有最大值4.5. 10分
而当x>7时,
所以当工厂生产600台产品时,盈利最大, 12分
知识点
已知数列



(1)求数列
(2)数列



正确答案
(1)

解析
(1)



经检验
综上 
(2)由(1)可知
=
=
=
知识点
10.已知函数


正确答案
解析
略
知识点
扫码查看完整答案与解析