- 直线、平面平行的判定与性质
- 共531题
如图,在四棱锥






(1)求证:

(2)求四棱锥
正确答案
见解析
解析
证明:(1) 连结













(2) 作

























知识点
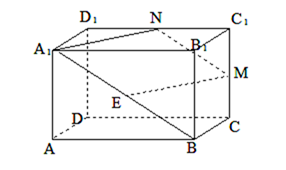
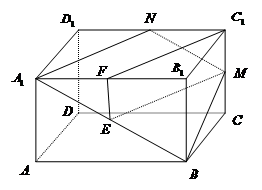
在直四棱柱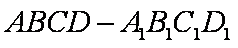
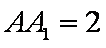
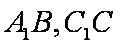
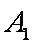
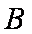
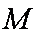
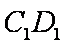
(1)求证: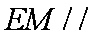
(2)求三棱锥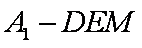
正确答案
见解析
解析
解析:
(1)(方法1 )证明:取A1B1的中点F,连EF,C1F
∵E为A1B中点∴EF∥ 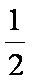
又∵M为CC1中点 ∴EF∥ C1M
∴四边形EFC1M为平行四边形 ∴EM∥FC1
而EM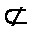
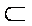
∴EM∥平面A1B1C1D1
(方法2 )可以证明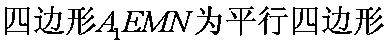
(2) 由(1)可得EM//A1N,又MN//A1E

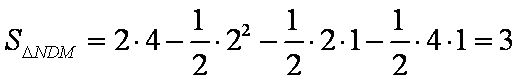
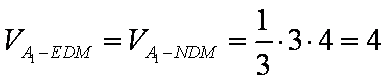
知识点
如图,多面体ABCDEFG中,四边形ABCD,CDEF都是边长为2的正方形,DE⊥平面ABCD,AG⊥平面ABCD,且AG=1。
(1)若P是BC的中点,证明AP∥平面BFG;
(2)求四面体ABEG的体积。
正确答案
见解析。
解析
(1)取BF中点Q,连PQ、GQ,则PQ∥CF,且PQ=
∵CDEF是正方形,DE⊥平面ABCD,
∴ CF⊥平面ABCD,
∴PQ⊥平面ABCD,
又AG⊥平面ABCD,
∴PQ∥AG,APQG为矩形,
∴AP∥GQ
∵QG

∴AP∥平面BFG
(2)∵AG⊥平面ABCD,∴AG⊥AD,
又ABCD是矩形,∴AB⊥AD
从而AD⊥平面ABG
又DE⊥平面ABCD,∴AG∥DE
∴
知识点
如果执行如图的程序框图,那么输出的值是( )
正确答案
解析
略
知识点
已知椭圆







(1)求椭圆
(2)过点







正确答案
见解析
解析
(1)






椭圆
(2)设


记



设存在定点



知识点
如图,在直三棱柱









(1)求证:

(2)求

正确答案
见解析
解析
(1)取
由已知可得


所以四边形
则
所以
(2)
又
所以
又

所以
所以得
得



知识点
下列命题中的假命题是
正确答案
解析
略
知识点
请考生在第22.23.24三题中任选一题做答,如果多做,则按所做的第一题记分.
22.如图,已知






(1)证明A,P,O,M四点共圆;
(2)求
23.选修4-4:坐标系与参数方程
过点



(1)写出直线
(2)求
(3)求
24.设对于任意实数x,不等式
(I)求m的取值范围;
(Ⅱ)当m取最大值时,解关于x的不等式:
22.如图,已知










(1)证明
(2)求
23.选修4-4:坐标系与参数方程
过点





(1)写出直线
(2)求
(3)求
24.设对于任意实数

(I)求m的取值范围;
(Ⅱ)当m取最大值时,解关于

正确答案
正确答案
正确答案
20.如图,四棱锥



(Ⅰ)证明:
(Ⅱ)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图所示的多面体中, 




(1)求证:平
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析