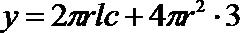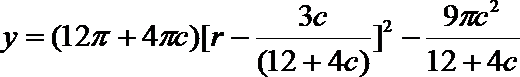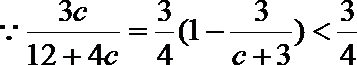- 直线、平面平行的判定与性质
- 共531题
15.若l,m为空间两条不同的直线,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若不等式
正确答案
2<b<4
解析
解析已在路上飞奔,马上就到!
知识点
6.如图是一个正三棱柱零件,面
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图, 四棱柱




(1)证明: 

(2)求三棱柱
正确答案
(1)证明
在RT△
在RT△
(2)
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)若函数


(2)当




(3)对于函数










正确答案
(1) 

设
则


(2)当

要使

即

只需






当


综上所述,当

当
(3)

且在
当

要使

只能满足


此时

即方程








此时

即
可得:


代入上式可得:
综上所述,
当


解析
解析已在路上飞奔,马上就到!
知识点
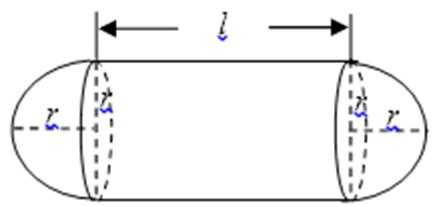
20.某加油站拟造如图所示的铁皮储油罐(不计厚度,长度单位:米),其中储油罐的中间为圆柱形,左右两端均为半球形,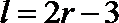
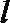
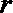

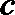

(1)写出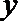

(2)求该储油罐的建造费用最小时的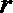
正确答案
(1)
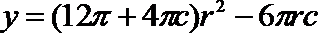
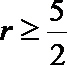
(2)
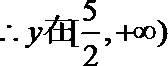
所以当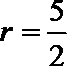
解析
解析已在路上飞奔,马上就到!
知识点
2.设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在三棱锥A—BOC中,


(I)求证:
(II)在线段CB上是否存在一点F,使得在CO上任取一点G均有AG//平面DEF?若存在,试确定F的位置;若不存在,请说明理由.
正确答案
(I)证明:因为

因为OB=OC=1,BC=2,所以

因为AO与BO相交于点O,所以CO垂直于平面AOB。
(II)适合条件的点F在在,且F是BC的中点,证明如下:
取BC的中点F,连结DF、EF。
因为D是OB的中点,所以DF//OC,同理,EF//AC,所以平面DEF//平面AOC。
因为AG在平面AOC内,所以AG//平面DEF。
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列{an}满足:
(1)求数列{an}的通项公式;
(2)当λ = 4时,若
(3)设Sn为数列{an}的前n项和.若对任意n∈N*,是否存在

正确答案
(1)当n=1时,a1=3.
当n≥2时,
因为
所以
①-②得
所以an=(2n+1)·λn-1(n≥2,n∈N*).
a1=3也适合上式,
所以an=(2n+1)·λn-1 (n∈N*).
(2)当λ=4时,
an=(2n+1)·4n-1
所以当
当

当
当

(3)Sn=3+5λ+7λ2+…+(2n+1)λn-1
当λ≠1时,Sn=3+5λ+7λ2+…+(2n+1)λn-1
λSn=3λ+5λ2+…+(2n-1)λn-1+(2n+1)λn
(1-λ)Sn=3+2(λ+λ2+λ3++…+λn-1)-(2n+1)λn=3+2×
假设对任意n∈N*,存在

但是当
当

矛盾,假设不成立
所以对任意n∈N*,不存在

解析
解析已在路上飞奔,马上就到!
知识点
3.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析