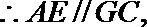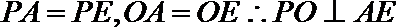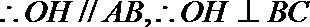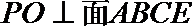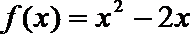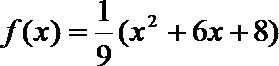- 直线、平面平行的判定与性质
- 共531题
18.如图,在直三棱柱


(1)求证:EF∥平面ABC;
(2)求证:平面

(3)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.一个四棱锥的三视图和直观图如图所示,其中俯视图中
(Ⅰ)求证:PB//平面AEC;
(Ⅱ)若F为侧棱PA上的一点,且


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知

正确答案
(2a,-a)
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆



(1)若椭圆、双曲线、抛物线在第一象限交于同一点
(2)若双曲线与抛物线在第一象限交于




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
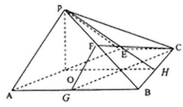
19.如图,在矩形
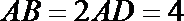
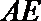
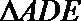
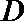
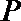

(Ⅰ)若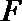

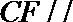
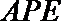
(Ⅱ)求证:面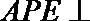
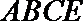
(Ⅲ)求三棱锥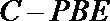
正确答案
(Ⅰ)
取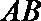
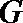
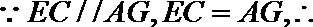
在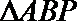
又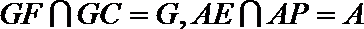
所以平面APE//平面FGC
又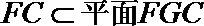
(Ⅱ)取AE中点O,连接PO,则
取BC的中点H,连OH,PH,
因为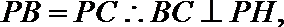
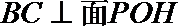
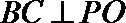
又BC与AE相交,可得
所以,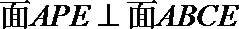
(Ⅲ)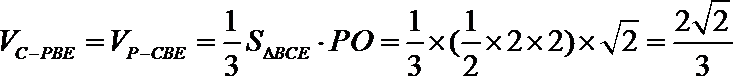
解析
解析已在路上飞奔,马上就到!
知识点
4.如果函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图所示,矩形








(1)求证:

(2)求证:

(3)求三棱锥
正确答案
(1)略;
(2)略;
(3)
解析
解析已在路上飞奔,马上就到!
知识点
16.定义域为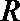
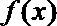
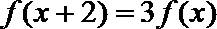
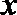
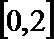
(1)当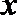
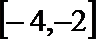
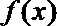
(2)当x∈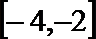
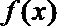
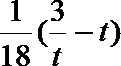
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
14.设不等式组





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析