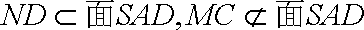- 直线、平面平行的判定与性质
- 共531题
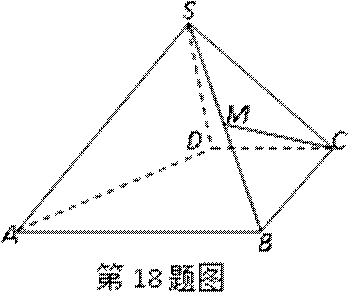
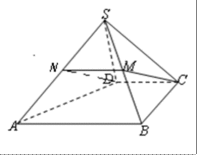
如图,在六面体



(1)
(2)
正确答案
见解析
解析
证明:(1)取线段



因为

所以

又




而

所以
(2)因为




所以

又



所以

所以
知识点
如图,四棱锥







(1)证明:
(2)证明:

正确答案
见解析。
解析
证明:
(1)由



又

(2)
取




又


所以

知识点
如图,在四棱锥E-ABCD中,底面ABCD为正方形, AE⊥平面CDE,已知AE=3,DE=4。
(1)若F为DE的中点,求证:BE//平面ACF;
(2)求直线BE与平面ABCD所成角的正弦值。
正确答案
见解析。
解析
(1)设AC与BD相交于G,连结GF。
正方形ABCD,





(2)解法一:过E点作EH⊥AD,垂足为H,连结BH1分








所以
Rt




解法二:









设直线BE与平面ABCD所成角为
所以直线BE与平面ABCD所成角的正弦值为
知识点
设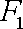
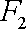

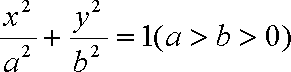
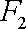


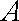
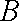
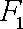
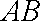


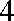
(1)求椭圆
(2)过椭圆
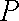
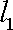

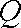
(ⅰ)若点

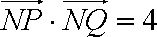
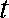
(ⅱ)过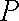
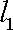
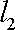


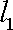
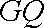

正确答案
见解析。
解析
(1)设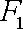
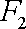
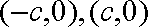
由题意得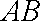
因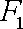
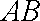

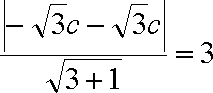
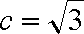
所以有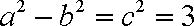
由题意知: 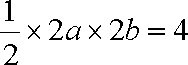
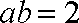
联立①②解得:
所求椭圆
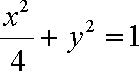
(2)由(1)知: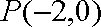
根据题意可知直线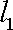
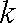
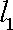
把它代入椭圆
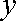
由韦达定理得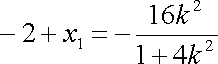
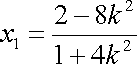
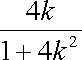
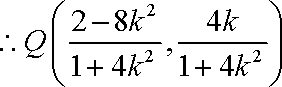

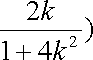
(ⅰ)当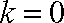
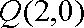

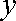
于是
由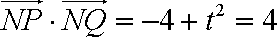
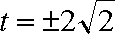
当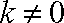

因为点

令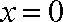
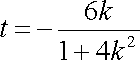
由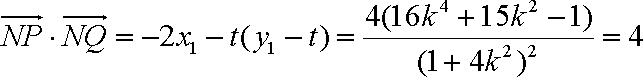
代入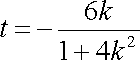
综上, 满足条件的实数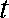
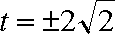
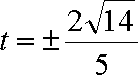
(ⅱ)设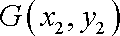
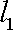
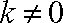
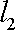
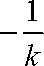
由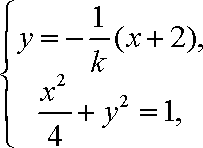
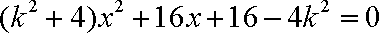
∵此方程有一根为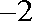
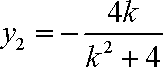
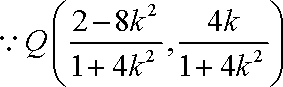
所以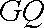
令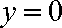
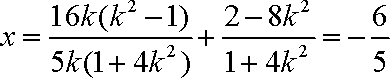
所以直线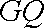

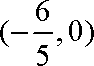
知识点
设正四棱锥的侧棱长为1,则其体积的最大值为 。
正确答案

解析
法1 设正四棱锥的底面边长为






法2 设正四棱锥的侧棱与底面所成角为






知识点
如图,在四棱锥P—ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M、N分别为PA、BC的中点,且PD=AD
(1)求证:MN//平面PCD;
(2)求证:平面PAC⊥平面PBD;
正确答案
见解析。
解析
(1)
取AD中点E,连接ME,NE. www.zxxk.com
由已知M,N分别是PA,BC的中点.
∴ME//PD,NE//CD……………………………………2分
又ME,

所以,平面MNE//平面PCD.…………………………4分
MN
所以,MN//平面PCD………………………………6分
(2)因为四边形ABCD为正方形.
所以AC⊥BD.
又PD⊥平面ABCD.AC
又BD
所以AC⊥平面PBD.…
AC
所以平面PAC⊥平面PBD…………………………………………………………12分
知识点
如图,四棱锥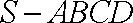
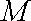
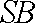
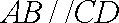


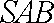
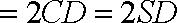
(1)证明:
(2)证明: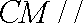
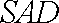
正确答案
见解析。
解析
(1)由
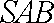
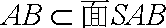

又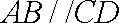

(2)
取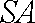
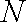
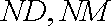
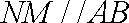
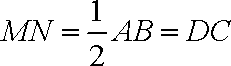
又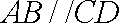
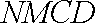
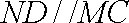
所以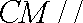
知识点
如图,在直三棱柱ABC﹣A1B1C1中,AC⊥BC,BC=BB1,D为AB的中点。
(1)求证:BC1⊥平面AB1C;
(2)求证:BC1∥平面A1CD。
正确答案
见解析。
解析
(1)∵三棱柱ABC﹣A1B1C1为直三棱柱
∴CC1⊥平面ABC;
又∵AC⊂平面ABC
∴CC1⊥AC
又∵AC⊥BC,CC1∩BC=C
∴AC⊥平面B1C1CB
又∵B1C⊂平面B1C1CB
∴B1C⊥AC
又∵BC=BB1,
∴平面B1C1CB为正方形,
∴B1C⊥BC1,又∵B1C∩AC=C
∴BC1⊥平面AB1C;
(2)
连接BC1,连接AC1于E,连接DE,E是AC1中点,
D是AB中点,则DE∥BC1,
又DE⊂面CA1D1,BC1⊄面CA1D1∴BC1∥面CA1D
知识点
如图,在斜三棱柱






(1)求
(2)证明EA1∥平面
正确答案
见解析。
解析
(1)解:过










因为


又因为



因此,由三垂线定理
因为


于是为


由于四边形
所以,


(2) 证明:设


在平行四边形

而EP





知识点
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,AB=5. 点D是AB的中点,
(1)求证:AC⊥BC1;
(2)求证:AC 1//平面CDB1;
(3)求异面直线 AC1与 B1C所成角的余弦值。
正确答案
见解析。
解析
(1)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
∴ AC⊥BC,
又因为 
又 





(2)
设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点
∵ DE


(3)∵ DE//AC1,∴ ∠CED为AC1与B1C所成的角,
在△CED中,ED=





∴ 
∴ 异面直线 AC1与 B1C所成角的余弦值
知识点
扫码查看完整答案与解析