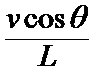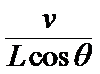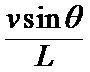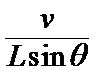- 运动的合成和分解
- 共81题
下列情形,保险公司可以解除保险合同的是( )。
A.甲向A保险公司投保车辆损失险,合同订立后,因该家用车辆转用于高速货物运输,增加了保险标的危险程度,甲将该事宜及时告知A公司
B.乙向B保险公司投保车辆损失险,后该车与其他车辆相撞,车灯受损,乙变造相应证明,夸大损失程度
C.丙向C保险公司投保车辆损失险,因为疏忽没有告知C公司工作人员其副驾驶座位的靠背已发生损坏
D.丁向D保险公司投保车辆损失险,但是其保险金额明显超过保险车辆的价值
正确答案
A
解析
[考点] 保险公司的合同解除权 [解析] 《保险法》第37条第1款规定,在合同有效期内,保险标的危险程度增加的,被保险人按照合同约定应当及时通知保险人,保险人有权要求增加保险费或者解除合同。可见,即使被保险人尽了及时通知的义务,保险公司也可以解除合同。故A项应选。 《保险法》第28条第3款规定,保险事故发生后,投保人、被保险人或者受益人以伪造、变造的有关匪明、资料或者其他证据,编造虚假的事故原因或者夸大损失程度的,保险人对其虚报的部分不承担赔偿或者给付保险金的责任。可见,投保人虚报损失的,仅免除保险人对虚报部分的责任,对整个合同,其并无解除权。故B项不选。 《保险法》第17条第4款规定,投保人因过失未履行如实告知义务,对保险事故的发生有严重影响的,保险人对于保险合同解除前发生的保险事故,不承担赔偿或者给付保险金的责任,但可以退还保险费。而C项中提到的“副驾驶座位的靠背已发生损坏”并不属于对保险事故的发生有严重影响的事实,故保险公司无解除权,C项不选。 保险金额超过保险车辆价值的,保险赔付以保险价值为最高限。该条件不构成保险公司解除合同的事由。故D项不选。
8.如图甲所示,杂技表演中,猴子沿竖直杆向上运动,其相对杆的v-t图象如图乙所示。人顶住杆(始终保持杆竖直)沿水平地面运动的x-t图象如图丙所示。若以地面为参考系,下列说法正确的是( )
正确答案
解析
本题是运动合成与分解中的基本问题,由题意可知
竖直杆在猴子上升过程中保持不动,没有位移,则A正确
根据水平方向匀速直线运动竖直方向的匀变速直线运动的合运动可知,猴子做匀变速曲线运动,B正确。由图像可知0s开始猴子竖直方向速度为8m/s,水平方向速度为4m/s,故C错误。1s时水平方向速度和竖直方向速度均为4m/s,D错误。
考查方向
解题思路
根据题意可知,竖直杆在猴子上升过程中保持不动,没有位移,猴子不做功
根据水平方向匀速直线运动竖直方向的匀变速直线运动的合运动可知,猴子做匀变速曲线运动。由图像可知0s开始猴子竖直方向速度为8m/s,水平方向速度为4m/s,合速度为

易错点
不能准确理解匀速直线运动与匀变速直线运动的合运动的特点
知识点
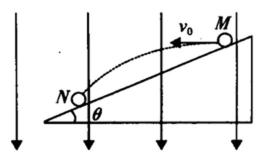
4.如下图所示,空间存在匀强电场,方向竖直向下,从绝缘斜面上的M点沿水平方向抛出一带电小球,最后小球落在斜面上的N点.已知小球的质量为m、初速度大小为v0、斜面倾角为θ,电场强度大小未知.则下列说法中正确的是( )
正确答案
解析
A、小球做类平抛运动,电场力既可向上也可向下,故小球带正电、负电都可以,A错;B、利用平抛知识有: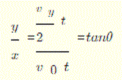
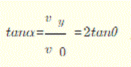
故选B.
考查方向
解题思路
由于是曲线运动,所以应该想到类平抛和动能定理。
易错点
不会用类平抛方法分析
知识点
4.如图所示,真空中的电场方向水平向右,从O点斜向上射入该电场中的带电油滴质量为m,其初速度大小为v,方向与电场方向成60°角,当油滴到达运动轨迹的最高点P时,速度大小仍为v。重力加速度为g,则对油滴从O点运动P点过程中,下列说法正确的是
正确答案
解析
试题分析:将油滴的运动分解为水平方向的匀加速运动和竖直方向的匀减速运动,则竖直方向的分速度为:

如果油滴带正电:水平方向:

如果油滴带负电:水平方向:




考查方向
解题思路
A将油滴的运动分解为水平方向的匀加速运动和竖直方向的匀减速运动,
B 根据动能定理,看合外力做功可以影响动能变化
C 除了重力以外力的功决定机械能的增减,可以判断机械能的增减
D 利用分运动中速度和位移的关系式,之后将分运动进行合成,可以解决OP之间的距离
易错点
不去分解合运动,分运动不能确定。
知识点
2.在离地高h处,以速度v0抛出一小球,不计空气阻力,已知h=
正确答案
解析
当小球竖直下抛时:

又
两式联立解之得,
当小球竖直上抛时:

由(2)(3)联立解之得,
故小球落地时间介于:
所以小球的落地时间不可能是
本题选不可能的,故选:D.
考查方向
解题思路
依题意,当小球竖直下抛时,小球落地时间最短,小球竖直上抛时,小球落地时间最长.小球落地时间介于两时间之间.分别求出最短时间和最长时间即可选出答案.
易错点
分清小球在空中运动的最长时间和最短时间两种情况是解决本题的关键.故只有分清物体运动过程、正确选择公式才可有效解决好运动学问题.
知识点
4.轻绳一端通过光滑的定滑轮与物块P连接,另一端与套在光滑竖直杆上的圆环

正确答案
解析
A、P先向下做加速运动,处于失重状态,后向上做减速运动,处于超重状态,故A错误.
B、将物块Q的速度分解为沿绳子方向和垂直于绳子的方向,在沿绳子方向的分速度等于P的速度.轻绳与杆的夹角为θ时,由速度的分解有:vP=vQcosθ,cosθ<1,则得vP<vQ.故B错误.
C、除重力以外其它力做的功等于物体机械能的增量,物块Q上升到与滑轮等高前,拉力做正功,机械能一直增加,物块Q上升到与滑轮等高时,机械能最大.故C正确.
D、当Q所受的合力为零时,速度最大,此时Q还没有到达到与滑轮等高的位置,故D错误.
故选:C
考查方向
动能定理的应用.
解题思路
根据加速度的方向分析P的状态.将物块Q的速度分解为沿绳子方向和垂直于绳子的方向,在沿绳子方向的分速度等于P的速度.结合平行四边形定则求出P、Q速度的关系.通过绳子拉力对Q物体的做功情况,判断物块Q机械能的变化,从而得出何时机械能最大.
易错点
除重力以外其它力做功等于机械能的增量。
知识点
23.某同学利用图示装置,验证以下两个规律:
①两物块通过不可伸长的细绳相连接,沿绳分速度相等;
②系统机械能守恒。 P、Q、R是三个完全相同的物块,P、Q用细绳连接,放在水平气垫桌上。物块R与轻质滑轮连接,放在正中间,a、b、c是三个光电门,调整三个光电门的位置,能实现同时遮光,整个装置无初速度释放。
(1)为了能完成实验目的,除了记录P、Q、R三个遮光片的
A.P、Q、R的质量M
B.两个定滑轮的距离d
C.R的遮光片到c的距离H
D.遮光片的宽度x
(2)根据装置可以分析出P、Q的速度大小相等,验证表达式为_______________;
(3)若要验证物块R与物块P的沿绳分速度相等,则验证表达式为_______________;
(4)若已知当地重力加速度g,则验证系统机械能守恒的表达式为_______________。
正确答案
(1)BCD
(2)
(3)
(4)
解析
(1)要验证物块R与物块P的沿绳分速度相等,首先应该测出它们的速度,即
(2)vP=vQ,即
(3)R沿绳子的分速度vRˊ=vRcosθ=vR




考查方向
1、考查速度的分解与合成。
2、考查实验中速度的测量方法。
3、考查机械能守恒的计算。
解题思路
1、首先清楚该实验中测量物块速度的原理:遮光片的长度与遮光时间的比值。
2、根据机械能守恒的计算式:mgH=


3、对R在C点的速度沿绳与垂直于绳的方向上分解,根据沿绳方向上的速度等于P的速度,得出物块R与物块P的沿绳分速度相等的验证表达式。
易错点
对实验原理理解不清楚。
知识点
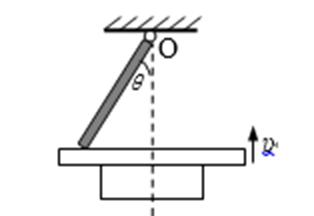
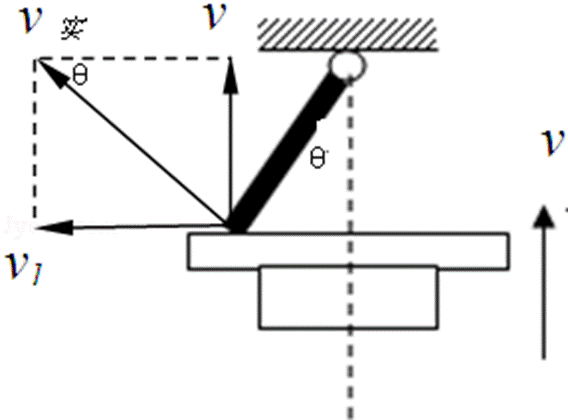
15.如图,长为L的直棒一端可绕固定轴O在竖直平面内转动,另一端搁在升降平台上,平台以速度υ匀速上升,当棒与竖直方向的夹角为θ时,棒的角速度为
正确答案
解析
棒与平台接触点的实际运动即合运动方向是垂直于棒指向左上,如图所示,
合速度v实=ωL,沿竖直向上方向上的速度分量等于v,即ωLsinθ=v,
所以ω=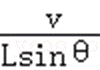
考查方向
解题思路
应清楚棒与平台接触点的实际运动即合运动方向是垂直于棒指向左上,竖直向上是它的一个分速度,把速度分解,根据三角形知识求解.
易错点
找合速度是本题的关键,应明白实际的速度为合速度.然后分解速度,做平行四边形,根据三角形求解
知识点
8.人用绳子通过定滑轮拉物体A,A穿在光滑的竖直杆上,当
正确答案
解析
将A的速度分解为沿绳子方向和垂直于绳子方向,如图所示,拉绳子的速度等于A沿绳子方向的分速度,
根据平行四边形定则得,实际速度为:v=
考查方向
解题思路
将A的速度分解为沿绳子方向和垂直于绳子方向,根据平行四边形定则求出A的实际运动的速度。
易错点
本题的关键知道速度的合成与分解遵循平行四边形定则,注意会画出正确的速度的分解图。
知识点
如图所示,宽L=2m、足够长的金属导轨MN和M′N′放在倾角为θ=30°的斜面上,在N和N′之间连接一个R=2.0Ω的定值电阻,在AA′处放置一根与导轨垂直、质量m=0.8kg、电阻r=2.0Ω的金属杆,杆和导轨间的动摩擦因数μ=
41. 求该过程中,通过电阻R的电量q;
42.杆通过OO′时的速度大小;
43.杆在OO′时,轻绳的拉力大小;
44.上述过程中,若拉力对杆所做的功为13J,求电阻R上的平均电功率。
正确答案
0.5C
解析
平均感应电动势

考查方向
解题思路
首先利用法拉第电磁感应定律求电量,通过牛顿第二定律求加速度,利用动能定理求变力做功。
易错点
在求解电量的时候移动要注意不能用切割磁感线的表达式求解
正确答案
3m/s
解析
几何关系:H/sinα-H=d,解得sinα=H/(H+d)=0.8,α=53°。杆的速度等于小车速度沿绳方向的分量:v1=vcosα=5.0×0.6m/s=3.0m/s。
考查方向
解题思路
首先利用法拉第电磁感应定律求电量,通过牛顿第二定律求加速度,利用动能定理求变力做功。
易错点
在求解电量的时候移动要注意不能用切割磁感线的表达式求解
正确答案
12.56N
解析
摩擦力Ff=μmgcosθ=



考查方向
解题思路
首先利用法拉第电磁感应定律求电量,通过牛顿第二定律求加速度,利用动能定理求变力做功。
易错点
在求解电量的时候移动要注意不能用切割磁感线的表达式求解
正确答案
2.0W
解析
动能定理:W+W安+(-mg·dsinθ)+(-Ff·d)=
考查方向
解题思路
首先利用法拉第电磁感应定律求电量,通过牛顿第二定律求加速度,利用动能定理求变力做功。
易错点
在求解电量的时候移动要注意不能用切割磁感线的表达式求解
扫码查看完整答案与解析