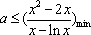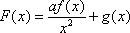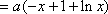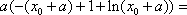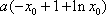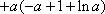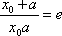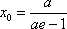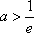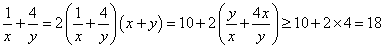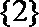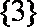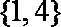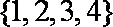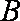- 平行公理
- 共21题
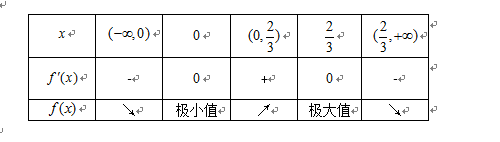
已知函数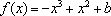
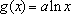
(1)若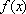
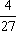
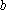
(2)若对任意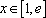
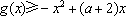

(3)若函数f(x)满足:在定义域内存在实数x0,使f(x0+k)= f(x0)+ f(k)(k为常数),则称“f(x)关于k可线性分解”. 设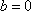
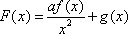

正确答案
见解析。
解析
(1)由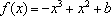
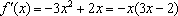
令
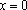

当
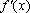
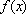
所以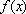
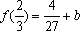
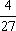
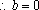
(2)由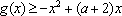
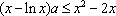
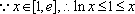
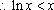
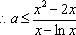
令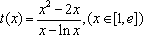
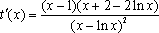
当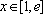
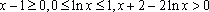
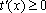
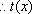
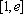
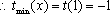
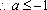
(3)证明:
由已知,存在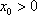
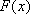
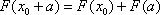
即:
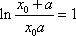
因为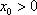
知识点
如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E、F分别在BC、AD上,EF∥AB,现将四边形ABEF沿EF折起,使得平面ABEF 
(1) 当



(2) 设BE=x,问当x为何值时,三棱锥A
正确答案
见解析。
解析
(1)存在

下面证明:
当









(2)因为平面ABEF







知识点
复数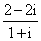
正确答案
-2i
解析
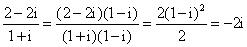
知识点
在空间,下列命题正确的是
正确答案
解析
由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以很容易得出答案。
知识点
设a,b,c是空间三条直线,
正确答案
解析
略
知识点
如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F。
(1)求证:AB为圆的直径;
(2)若AC=BD,求证:AB=ED。
正确答案
略。
解析
(1)∵PG=PD,∴∠PDG=∠PGD,
∵PD为切线,∴∠PDA=∠DBA,
∵∠PGD=∠EGA,
∴∠DBA=∠EGA,
∴∠DBA+∠BAD=∠EGA+∠BDA,
∴∠NDA=∠PFA,
∵AF⊥EP,
∴∠PFA=90°。
∴∠BDA=90°,
∴AB为圆的直径;
(2)连接BC,DC,则
∵AB为圆的直径,
∴∠BDA=∠ACB=90°,
在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,
∴Rt△BDA≌Rt△ACB,
∴∠DAB=∠CBA,
∵∠DCB=∠DAB,
∴∠DCB=∠CBA,
∴DC∥AB,
∵AB⊥EP,
∴DC⊥EP,
∴∠DCE为直角,
∴ED为圆的直径,
∵AB为圆的直径,
∴AB=ED。
知识点
已知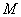
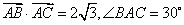
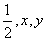
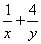
正确答案
解析
由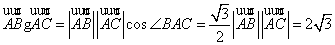
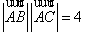
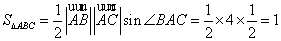
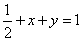
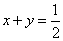
知识点
已知函数

(1)当

(2)设函数


正确答案
见解析
解析
(1)当


令

令

∴



(2)
要使函数


即:
解得:
知识点
已知全集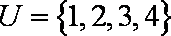
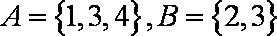
正确答案
解析
由韦恩图知: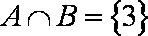
知识点
已知

(1)若


(2)求
(3) 设



正确答案
。
解析
(1) 


经检验, 
(2)
1) 当


2)当
① 若




② 若



综上所述,当


当



(3)当


易知

注意到
故由题设知

故

知识点
扫码查看完整答案与解析