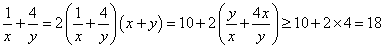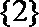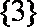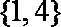- 平行公理
- 共21题
如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E、F分别在BC、AD上,EF∥AB,现将四边形ABEF沿EF折起,使得平面ABEF 
(1) 当



(2) 设BE=x,问当x为何值时,三棱锥A
正确答案
见解析。
解析
(1)存在

下面证明:
当









(2)因为平面ABEF







知识点
已知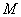
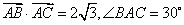
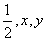
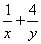
正确答案
解析
由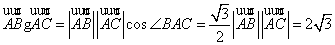
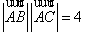
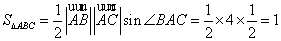
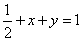
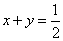
知识点
已知函数

(1)当

(2)设函数


正确答案
见解析
解析
(1)当


令

令

∴



(2)
要使函数


即:
解得:
知识点
已知全集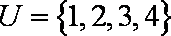
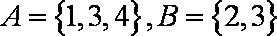
正确答案
解析
由韦恩图知: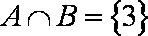
知识点
已知

(1)若


(2)求
(3) 设



正确答案
。
解析
(1) 


经检验, 
(2)
1) 当


2)当
① 若




② 若



综上所述,当


当



(3)当


易知

注意到
故由题设知

故

知识点
扫码查看完整答案与解析