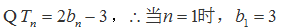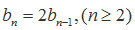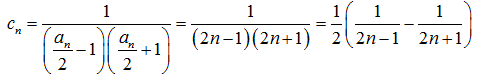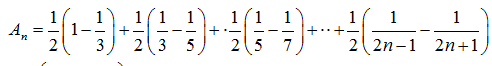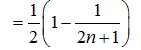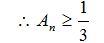- 裂项相消法求和
- 共32题
19.对于数列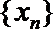
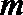
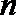
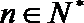
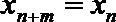
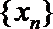
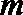
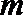
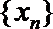
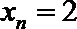
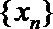
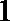
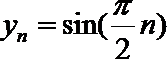
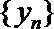
(Ⅰ)设数列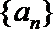
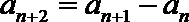
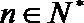
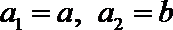
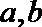
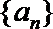
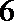
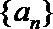
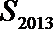
(Ⅱ)设数列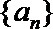
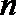
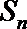
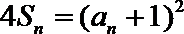
①若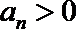
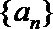
②若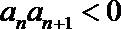
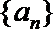
(Ⅲ)设数列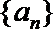
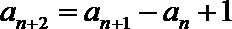
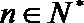
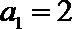
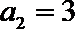
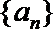
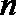
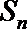
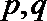
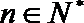
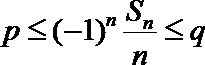
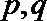
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知数列




正确答案
解析








考查方向
解题思路
详见解析
易错点
不能够想到

知识点
18. 已知数列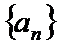
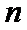
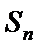
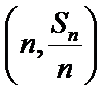
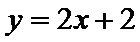
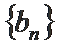
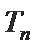
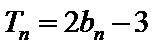
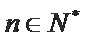
(Ⅰ)求数列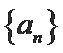
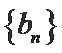
(Ⅱ)设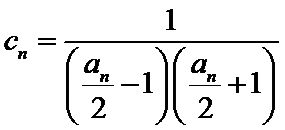
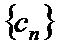
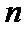
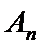
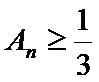
正确答案
(1)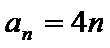
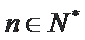
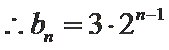
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
解:(Ⅰ)由题意,得 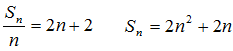
当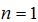
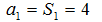
当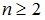
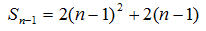
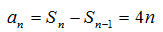
综上,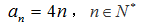
又
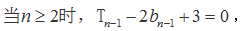
数列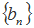
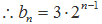
(Ⅱ)
考查方向
解题思路
本题考查数列问题,解题步骤如下:
1、利用an与Sn的关系求解。
2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。
知识点
6.定义







正确答案
解析
由“均倒数”为

则
考查方向
本题主要考查数列的综合运算
解题思路
(1)求出an;(2)求出bn,利用裂项相消法求和,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在求an时发生错误。
知识点
19. 设数列






(1)求证:数列

(2)令








正确答案
见解析
解析
解:(1)当


代入

而
∴数列
∴


又
(2)当



∴
故
当

若
则等式


若


∵



∴当且仅当


综上可知,当


当


考查方向
解题思路
利用

易错点
忽略n的范围的讨论。
知识点
扫码查看完整答案与解析