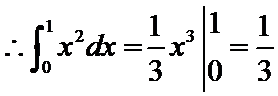- 二项式定理的应用
- 共36题
6.设a=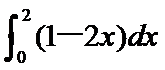
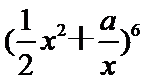
正确答案
解析
由已知得a=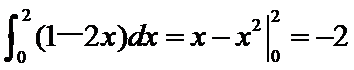
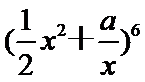
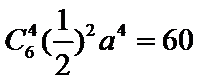
考查方向
解题思路
先根据定积分求出a的值为-2,再利用二项展开式解得常数项为60
因此A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
二项式定理的展开式易出错
知识点
设(1-x)n=a0+a1x+a2x2+…+anxn,n∈N*,n≥2.
33.设n=11,求|a6|+|a7|+|a8|+|a9|+|a10|+|a11|的值;
34.设bk=

正确答案
(1)1024;
解析
解:(1)因为ak=(-1)k 
当n=11时,|a6|+|a7|+|a8|+|a9|+|a10|+|a11|=
=
考查方向
解题思路
本题考查二项式定理和性质,解题步骤如下:
(1)由二项式定理可得ak=(-1)k
=(-1)k-1 

易错点
二项式定理和性质不会熟练应用,容易计算错误
正确答案
(2)1
解析
(2)bk=


当1≤k≤n-1时,bk=(-1)k+1 





当m=0时,|

当1≤m≤n-1时,
Sm=-1+

所以|

考查方向
解题思路
本题考查二项式定理和性质,解题步骤如下:
(2)由组合数的阶乘公式可得bk= (-1)k+1 
=(-1)k-1 

易错点
二项式定理和性质不会熟练应用,容易计算错误
12.二项式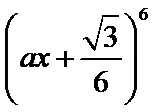
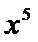
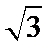
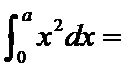
正确答案
解析
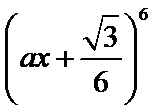
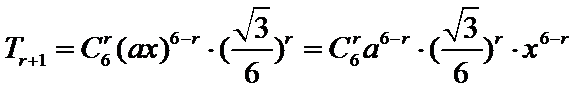
则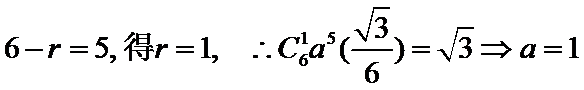
考查方向
解题思路
1、写出二项展开式,确定r,直接计算得到a,
2、根据定积分求出结果
易错点
本题易错在二项展开式记忆错误
知识点
10. 已知(
正确答案
解析








故A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
含x2与x3的项的系数,再根据绝对值之比为1:6,算得
易错点
确定项的系数时计算易出错。
知识点
13.已知


正确答案
2
解析
原式可变为

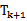









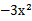


考查方向
解题思路
先展开






易错点
在利用匹配关系中,容易找错

知识点
扫码查看完整答案与解析