- 导数的加法与减法法则
- 共610题
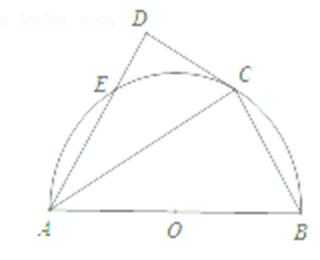
已知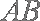

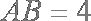


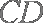
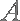
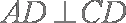

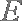
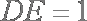
(1)求证: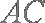
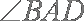
(2)求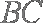
正确答案
见解析
解析
(1)连结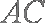
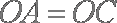
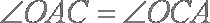
因为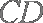
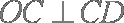
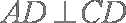
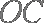
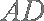
所以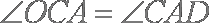
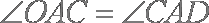
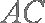
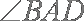
(2)由(1)知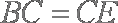
连结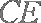
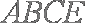

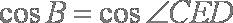
所以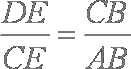
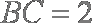
知识点
已知函数
(1)若函数


(2)当



正确答案
见解析。
解析
(1)
(2)
(i)当a≤1时,f (x) 在区间[1,3]上是单调增函数,最小值为f (1)。
由于f (1)=4,即

(ii)当
f (a)=4,即
解得 

(iii)当a≥3时,f (x)在区间(1,a)上是减函数,f (3)为最小值。
f (3)=4,即

综上所述,
知识点
在数列




(1) 求证:数列
(2) 求数


正确答案
见解析。
解析
(1)因为

切线方程为
又因为过点(

即
所以
即数列

(2)由(1)得

则


知识点
设

(1)若








(2)请类比(1),针对等差数列提出相应的真命题(不必证明),并写出相应的等差数列的前
正确答案
见解析。
解析
(1)①设
则设
(

当



故

当
证法一:对任意的


证法二:

注:此处用反证法,或证明
②设
对于任意



(2)设



①

②当


若

若

③当


知识点
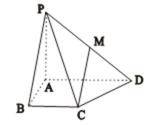
如图,在底面是直角梯形的四棱锥P—ABCD中,AD∥BC,∠DAB=90º,PA⊥平面ABCD,PA=AB=BC=1,AD=2,M是PD的中点。
(1)求证:MC∥平面PAB;
(2)在棱PD上求一点Q,使二面角Q—AC—D的正切值为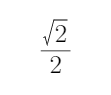
正确答案
见解析。
解析
(1)过M作MN∥PA交AD于N,连接CN,
∵PA⊥平面ABCD且MP=MD,∴MN⊥平面ABCD且NA=ND,
∴AB=BC=AN=CN=1,
又∠NAB=90º,DA∥BC,∴四边形ABCN为正方形,
∴AB∥NC,∴平面PAB∥平面MNC。
∴MC∥平面PAB。
(2)在(1)中连接NB交AC于O,则NO⊥AC,连接MO,∵MN∥平面ABCD,
MO⊥AC,∴∠MON就是二面角M—AC—D的平面角,∵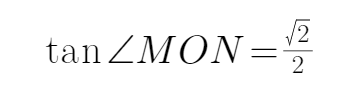
∴点M就是所求的Q点。
知识点
扫码查看完整答案与解析