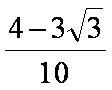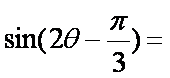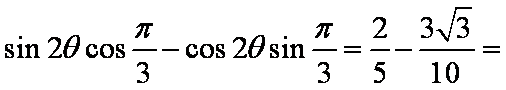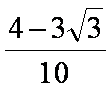导数的加法与减法法则
共610题

· 导数的加法与减法法则

导数的加法与减法法则
共610题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

已知

（1）求的最小正周期及单调递减区间；

（2）当时，求的最大值和最小值，并求出相应的的值。

正确答案

见解析

解析

解析：（1），减区间为：，（或者）开闭区间均可。

（2）当时，；当时，。

知识点

导数的加法与减法法则

题型：简答题

简答题 · 10 分

如图，是⊙的一条切线，切点为，都是⊙的割线，。

（1）证明：；

（2）证明：。

正确答案

见解析

解析

（1）由切割线定理知,又，得

（2）由得∽，所以

又四边形GEDF四点共圆，所以

故,所以

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

定义运算：，将函数的图像向左平移（）个单位，所得图像对应的函数为偶函数，则的最小值是（）

正确答案

解析

试题分析：，将函数化为再向左平移（）个单位即为: 又为偶函数,由三角函数图象的性质可得,即时函数值为最大或最小值,即或,所以 ,即,又,所以的最小值是.

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

已知分别为双曲线（a＞0,b＞0）的左、右焦点，为双曲线左支上的任意一点，若的最小值为，则双曲线离心率的取值范围是（）

正确答案

解析

试题分析：是左、右焦点，为双曲线左支上的任意一点,所以

代入得: ,当且仅当时取等号,即,又点是双曲线左支上任意一点,所以 ,即， .

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

已知向量=（）,=()(>0),函数f(x)=.,且函数f(x)的图象中任意两相邻对称轴间的距离为π。

（1）求的值；

（2）已知在△ABC中，角A,B,C所对的边分别为a,b,c,f(C),且c=,△ABC的面积S=，求a+b的值。

正确答案

（1）（2）10

解析

解析：（1）由题知

∵函数f(x)的图象中任意两相邻对称轴间的距离为π

∴T=2π从而得

故ω=。

（2）由（1）知f(x)=sin(x-)∴f(C)=sin(C-)

∵0<C<π∴-<C-<

∴C-=从而得C=

∵S=absinC=∴ab=8

又由余弦定理得

∴=100∴a+b=10.

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

已知，则 .

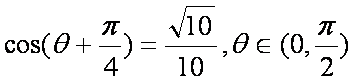
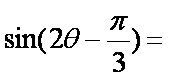
正确答案

解析

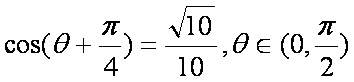
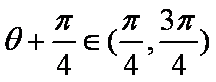
解析：由，得，

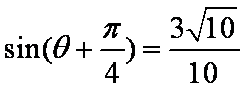
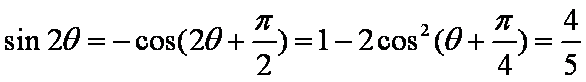
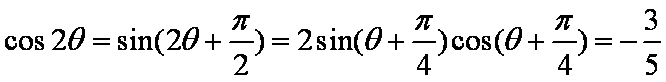
则，所以，

，

所以，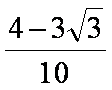

故答案为：

知识点

导数的加法与减法法则

题型：简答题

简答题 · 14 分

已知函数

（1）若在区间上是增函数，求实数a的取值范围；

（2）若的一个极值点，求上的最大值；

（3）在（2）的条件下，是否存在实数b，使得函数的图象恰有3个交点，若存在，请求出实数b的取值范围；若不存在，试说明理由。

正确答案

见解析

解析

（1）

，

即

则必有 …………5分

（2）依题意

即

…………6分

令

得则

当x变化时，的变化情况如下表：

在[1，4]上的最大值是 …………10分

（3）函数的图象与函数f（x）的图象恰有3个交点，

即方程恰有3个不等实根…………12分

是其中一个根，

有两个非零不等实根，

…………14分

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

数列满足，且对任意的正整数都有，则= .

正确答案

解析

试题分析：数列对任意的正整数都有,及令得:

所以上面各式相加得: 所以即所以

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

已知直线和平面，则的一个必要条件是

A，

B，

C，

D与成等角

正确答案

解析

解析：A：m、n可以都和平面垂直，不必要

B：m、n可以都和平面平行，不必要

C：n不一定要在平面内，不必要

D，平行所以成的角一定相等，但反之如果两直线相交成等边三角形之势则不平行，所以是必要非充分

故选D

知识点

导数的加法与减法法则

题型：简答题

简答题 · 10 分

已知极坐标的极点在平面直角坐标系的原点处，极轴与轴的正半轴重合，且长度单位相同，直线的极坐标方程为：,点，参数.

（1）求点轨迹的直角坐标方程；

（2）求点到直线距离的最大值。

正确答案

见解析。

解析

（1）且参数，

所以点的轨迹方程为。

（2）因为，所以，

所以，所以直线的直角坐标方程为。

法一：由(Ⅰ) 点的轨迹方程为，圆心为，半径为2.

，所以点到直线距离的最大值

法二：，当，，即点到直线距离的最大值.

知识点

导数的加法与减法法则

继续学习学习下一知识点

下一知识点 : 导数的乘法与除法法则

百度题库 > 高考 > 文科数学 > 导数的加法与减法法则

扫码查看完整答案与解析