- 导数的加法与减法法则
- 共610题
12.等比数列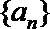

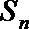
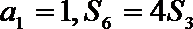
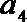
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列






(1)求
(2)求数列
(3)是否存在正整数




正确答案
(1)解:∵

∴
∴ 
∴ 
(2)解法1:由

∴ 数列


∴ 
∴ 
当

而
∴ 
解法2:由

∴
当

①

∴
∴
∴ 数列


∴ 
而
∴ 
(3)解:由(2)知

假设存在正整数



则
即
∵ 
∴
得

解得


∴ 不存在正整数



解析
解析已在路上飞奔,马上就到!
知识点
6.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 如图,


















正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知:向量
(1)若
(2)设函数

正确答案
(1)由
由

(2)

∴当


解析
解析已在路上飞奔,马上就到!
知识点
10.定义在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,例如解析式为
(1)
(2)
(3)
那么函数解析式为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设p:实数x满足x2-4ax+3a2<0,其中a<0;q:实数x满足x2-x-6≤0,或x2+2x-8>0,且
正确答案
设A={x|p}={x|x2-4ax+3a2<0,a<0}={x|3a<x<a,a<0},
B={x|q}={x|x2-x-6≤0或x2+2x-8>0}={x|x2-x-6≤0}∪{x|x2+2x-8>0}
={x|-2≤x≤3}∪{x|x<-4或x>2}=
∵

则


∴
则
(法二)即:
可得-
解析
解析已在路上飞奔,马上就到!
知识点
16.在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,三边a、b、c成等差数列,且B=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析





























