导数的加法与减法法则
共610题

· 导数的加法与减法法则

导数的加法与减法法则
共610题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

已知全集U＝{0,1,2,3,4,5,6,7,8,9}，集合A＝{0,1，3,5,8}，集合B＝{2,4,5,6,8}，则(UA)∩(UB)＝(　　)

A{5,8}

B{7,9}

C{0,1,3}

D{2,4,6}

正确答案

解析

由已知条件可得UA＝{2,4,6,7,9}，UB＝{0,1,3,7,9}，

所以(UA)∩(UB)＝{7,9}，故选B

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

设全集为R, 函数的定义域为M, 则为（）

A(－∞,1)

B(1, + ∞)

正确答案

解析

,所以选B

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

如图, AB与CD相交于点E, 过E作BC的平行线与AD的延长线相交于点P. 已知, PD = 2DA = 2, 则PE = （）.

正确答案

解析

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

若点(x,y)位于曲线y = |x|与y = 2所围成的封闭区域, 则2x－y的最小值为（）

A－6

B－2

正确答案

解析

的图像围成一个三角形区域，3个顶点的坐标分别是 (0,0),(-2,2),(2,2). 且当取点(-2,2)时，2x – y = - 6取最小值。所以选A

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

已知函数f（x）=x-3ax+3x+1。

（1）设a=2，求f（x）的单调期间；

（2）设f（x）在区间（2,3）中至少有一个极值点，求a的取值范围。

正确答案

见解析。

解析

（1）

（2）

①式无解，②式的解为，

因此的取值范围是.

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

已知是虚数单位，若，则

正确答案

解析

由得，，

故答案选A

知识点

导数的加法与减法法则

题型：简答题

简答题 · 13 分

从某居民区随机抽取10个家庭，获得第个家庭的月收入（单位：千元）与月储蓄（单位：千元）的数据资料，算得

（1）求家庭的月储蓄对月收入的线性回归方程；

（2）判断变量与之间是正相关还是负相关；

（3）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄。

附：线性回归方程中，

其中为样本平均值，线性回归方程也可写为.

正确答案

见解析

解析

（1）由题意知

n＝10，，，

又lxx＝＝720－10×82＝80，

lxy＝＝184－10×8×2＝24，

由此得，＝2－0.3×8＝－0.4，

故所求回归方程为y＝0.3x－0.4.

（2）由于变量y的值随x的值增加而增加(b＝0.3＞0)，故x与y之间是正相关。

（3）将x＝7代入回归方程可以预测该家庭的月储蓄为y＝0.3×7－0.4＝1.7(千元)。

知识点

导数的加法与减法法则

题型：简答题

简答题 · 15 分

设函数

（1）求的单调区间

（2）求所有实数，使对恒成立。注：e为自然对数的底数。

正确答案

（1）增区间为（0，a）,减区间为（a,+∞）（2）

解析

（1）解：因为，其中，

所以。

由于，所以的增区间为（0，a）,减区间为（a,+∞）

（2）证明：由题意得，，即

由（Ⅰ）知在[1,e]恒成立，

要使对恒成立，

只要，解得

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

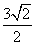
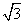
已知正四棱锥O－ABCD的体积为，底面边长为，则以O为球心，OA为半径的球的表面积为__________。

正确答案

24π

解析

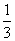
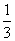
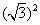
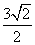
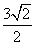
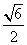
如图所示，在正四棱锥O－ABCD中，VO－ABCD＝×S正方形ABCD·|OO1|＝××|OO1|＝，

∴|OO1|＝，|AO1|＝，

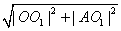
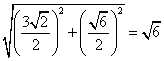
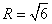
在Rt△OO1A中，OA＝＝，即，

∴S球＝4πR2＝24π.

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

在复平面上，复数的共轭复数的对应点所在的象限是（）

A第一象限

B第二象限

C第三象限

D第四象限

正确答案

解析

略。

知识点

导数的加法与减法法则

继续学习学习下一知识点

下一知识点 : 导数的乘法与除法法则

百度题库 > 高考 > 文科数学 > 导数的加法与减法法则

扫码查看完整答案与解析