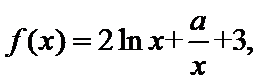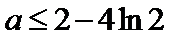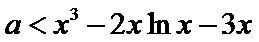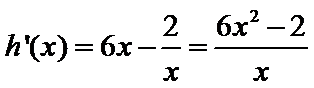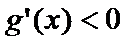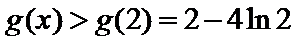- 导数的加法与减法法则
- 共610题
12.设函数


正确答案
解析
由



考查方向
解题思路
本题综合性较强,考查的知识点包括函数的奇偶性及单调性和不等式的解法,本题解法中用到了偶函数的一个性质,即:

易错点
根据函数的奇偶性和单调性之间的关系,将不等式进行转化得到结论.
知识点
4.设


正确答案
解析
因为




考查方向
解题思路
点


易错点
原函数与反函数定义域值域的对应关系
知识点
已知过原点的动直线



27.求圆
28.求线段


29.是否存在实数



正确答案
(1)
解析
(1)由

∴ 圆

考查方向
解题思路
第一问,将圆的普通方程化为标准方程,写出圆心坐标
易错点
轨迹方程中,不能忽略了x的取值范围问题。第三问不能忽略直线过轨迹端点时的值。
正确答案
(1)

解析
(2)设
∵ 点


∴ 

∴ 线段


考查方向
解题思路
第二问,设出中点坐标,利用垂直关系即可找到轨迹方程。
易错点
轨迹方程中,不能忽略了x的取值范围问题。第三问不能忽略直线过轨迹端点时的值。
正确答案
(3)
解析
(3)由(2)知点









当直线








考查方向
解题思路
第三问,利用数形结合,当相切或者过轨迹端点时,只有一个交点,列出相应的方程,可求解。
易错点
轨迹方程中,不能忽略了x的取值范围问题。第三问不能忽略直线过轨迹端点时的值。
15.一个二元码是由0和1组成的数字串


已知某种二元码
其中运算

现已知一个这种二元码在通信过程中仅在第

正确答案

解析
由题意得相同数字经过运算后为










考查方向
解题思路
根据二元码的码元满足的方程组,及运算规则,将k的值从1至7逐个验证即可。
易错点
新定义运算的阅读能力,阅读分析理解能力弱
知识点
6.一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )
正确答案
D
解析
如图所示,截去部分是正方体的一个角,其体积是正方体体积的


考查方向
解题思路
由于三视图能有效的考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般常与几何体的表面积与体积交汇.由三视图还原出原几何体,是解决此类问题的关键.
易错点
分清切割部分与剩余部分体积
知识点
13.已知函数
正确答案
-2
解析
由

考查方向
解题思路
本题考查内容单一,由
易错点
计算的准确性
知识点
12.已知定义在实数集







正确答案
解析
构造函数













考查方向
解题思路
构造函数再利用已知条件即可解出。
易错点
不会构造函数求解。
知识点
12.设a∈R,函数
正确答案
得a=-1,f(x)+3=0的解为-2。
解析
解:∵函数f(x)是奇函数,
∴f(0)=0,则20+a=1+a=0,得a=-1,
若x<0,则-x>0,
则f(-x)=2-x-1=-f(x),
则f(x)=1-2-x,x<0,
即g(x)=1-2-x,x<0,
由f(x)+3=0得f(x)=-3,
若x≥0,由f(x)=-3得2x-1=-3,得2x=-2,此时方程无解,
若x<0,由f(-x)=-3得1-2-x=-3,
得2-x=4,即-x=2,得x=-2,
故答案为:-2
考查方向
解题思路
根据函数奇偶性的性质建立方程关系进行求解即可.
易错点
奇函数的性质应用时候问题。
知识点
函数
25.当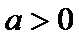
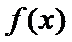
26.若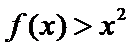
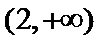
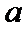
正确答案
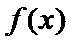
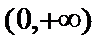
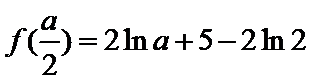
解析
(1)由题意: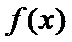
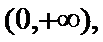
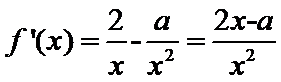
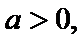
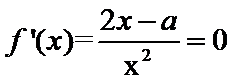
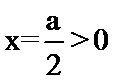
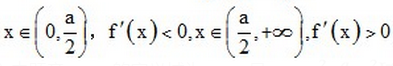
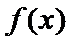
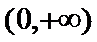
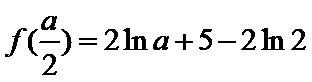
考查方向
解题思路
先求导再判断导数的符号。
易错点
求导弄错。
正确答案
解析
(2)因为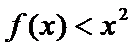
又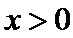
令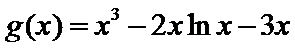
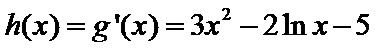
因为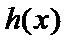
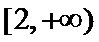
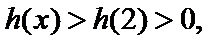
所以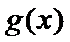
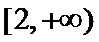
令
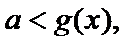
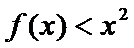
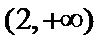
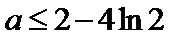
考查方向
解题思路
构造函数再利用导数这个工具即可解出。
易错点
不会构造函数去求解。
已知函数

25.讨论函数
26.若函数





27.证明对于任意n∈N,n≥2有:
正确答案
详见解析
解析
解:



当




当



若


故函数


考查方向
利用导数求函数的单调性
导数与函数的综合应用
解题思路
先求导,然后讨论参数,分类求出单调区间和单调性
易错点
求导错误,分类讨论错误
正确答案
详见解析
解析
求导数:
∴
所以

由于

令
当


∴


故


考查方向
导数与不等式的综合题
已知不等式成立,求参数的取值范围
解题思路
求导数,然后构造函数,分类讨论求出参数的取值范围
易错点
分类讨论错误,构造不出来恰当的函数
正确答案
详见解析
解析
证明:由当






∴当




∴

考查方向
函数与不等式的综合题
解题思路
利用函数的单调性证明不等式
易错点
不能够造出恰当的函数,不能正确的讨论函数的单调性
扫码查看完整答案与解析