- 余弦定理
- 共104题
1
题型:填空题
|
16.在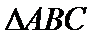
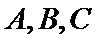
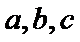
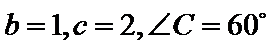
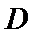
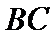
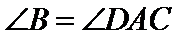
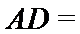
正确答案
解析
在三角形ABC中由正弦定理可以求出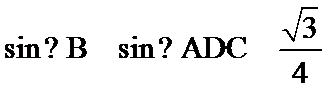
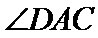
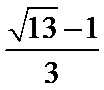
考查方向
正余弦定理解三角形。
解题思路
本题考查正余弦定理解三角形的能力,解题步骤如下:先用正弦定理求出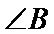
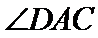
易错点
不会灵和应用定理解答。
知识点
正弦定理余弦定理三角形中的几何计算
1
题型:填空题
|
15.在



则
正确答案
解析
因为


所以

考查方向
余弦定理;解直角三角形
解题思路
先根据余弦定理表示出
易错点
利用定理进行恒等变换时错误
知识点
正弦定理余弦定理三角形中的几何计算
1
题型:简答题
|
已知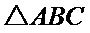
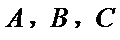
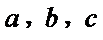
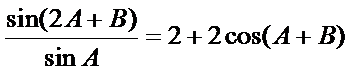
17.求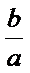
18.若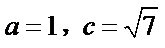
第(1)小题正确答案及相关解析
正确答案
(1)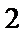
解析
(Ⅰ)∵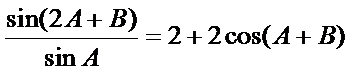
∴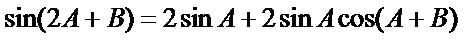
∴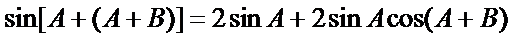
∴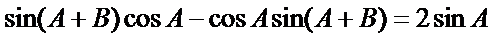
∴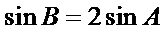
∴
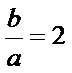
考查方向
本题主要考查了三角恒等变换,正余弦定理,以及三角形面积。
解题思路
1)第一问中用两角和差公式和三角恒等变换化简得到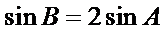
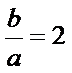
2)第二问中用倍余弦定理得到一个角,在用三角形面积公式求得面积。
易错点
1)第一问中想不到将角
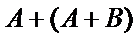
2)第二问中用余弦定理求角时容易将特殊角记错。
第(2)小题正确答案及相关解析
正确答案
(2)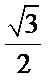
解析
(Ⅱ)∵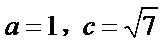
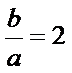
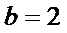
∴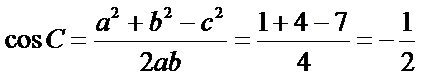
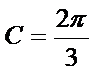
∴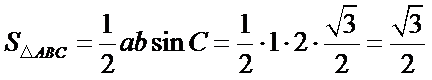
即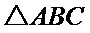
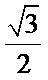
考查方向
本题主要考查了三角恒等变换,正余弦定理,以及三角形面积。
解题思路
1)第一问中用两角和差公式和三角恒等变换化简得到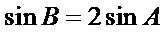
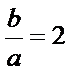
2)第二问中用倍余弦定理得到一个角,在用三角形面积公式求得面积。
易错点
1)第一问中想不到将角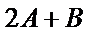
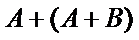
2)第二问中用余弦定理求角时容易将特殊角记错。
1
题型:简答题
|
17.在



(Ⅰ)求证:
(Ⅱ)若


正确答案
见解析
知识点
余弦定理
1
题型:
单选题
|
4.ΔABC的内角A,B,C的对边分别为a,b,c.已知
则b=( )
正确答案
A
知识点
余弦定理
下一知识点 : 余弦定理的应用
扫码查看完整答案与解析