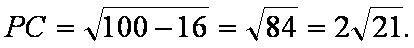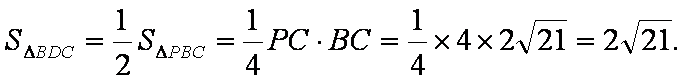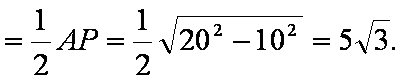- 余弦定理的应用
- 共29题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
位于A处的雷达观测站,发现其北偏东45°,与



(1)求
正确答案
(1)

解析
解析:(1)

(2)利用余弦定理
该船以匀速直线行驶了20分钟的路程为
该船的行驶速度
知识点
设




正确答案
解析


因为



知识点
若

正确答案
d
解析
(探究性理解水平∕两角差的正弦、正弦函数的性质)由题得原方程为:




知识点
若三条线段的长分别为3、5、7,则用这三条线段( )
正确答案
解析
解:∵3+5=8且8>7,
∴三条线段可以组成一个三角形,且该三角形的最大角为7所对的角
设最大角为α,根据余弦定理得cosα= <0
结合α∈(0,π),得α为钝角,所以此三角形为钝角三角形
故选:C
知识点
正三角形




正确答案
解析
略
知识点
已知△ABC的三内角A、B、C所对的边的长分别为a、b、c,设向量
(1)求
(2)若
正确答案
见解析。
解析
(1)∵
∴
由余弦定理得:
又∵

(2)∵
∴

∴a<b ∴A<B
∴


∴

知识点
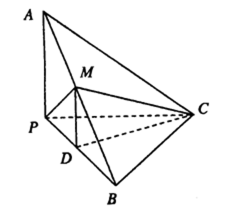
如图,三棱锥A—BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形。
(1)求证:DM//平面APC;
(2)求 证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D—BCM的体积。
正确答案
见解析。
解析
(1)∵M为AB中点,D为PB中点,
∴MD//AP, 又∴MD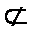
∴DM//平面APC
(2)∵△PMB为正三角形,且D为PB中点。
∴MD⊥PB
又由(1)∴知MD//AP, ∴AP⊥PB
又已知AP⊥PC ∴AP⊥平面PBC,
∴AP⊥BC, 又∵AC⊥BC
∴BC⊥平面APC, ∴平面ABC⊥平面PAC
(3)∵AB=20
∴MB=10 ∴PB=10
又BC=4,
∴
又MD
∴VD-BCM=VM-BCD=
知识点
19.


(1)求角
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析