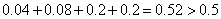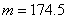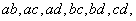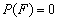- 统计与统计案例
- 共590题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
从某学校的
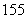
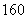
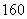
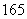

(1)求第七组的频率;
(2)估计该校的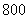

(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为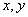
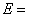
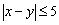
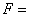
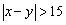
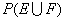
正确答案
见解析。
解析
(1)第六组的频率为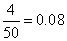

(2)身高在第一组[155,160)的频率为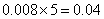
身高在第二组[160,165)的频率为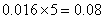
身高在第三组[165,170)的频率为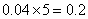
身高在第四组[170,175)的频率为
由于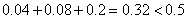
估计这所学校的800名男生的身高的中位数为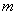
由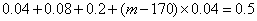
所以可估计这所学校的800名男生的身高的中位数为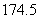
由直方图得后三组频率为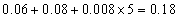
所以身高在180cm以上(含180cm)的人数为
(3)第六组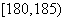
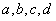

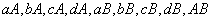
因事件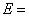
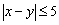
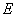
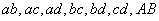
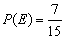
由于

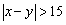
由于事件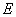
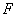

知识点
下图为某地区2012年1月到2013年1月鲜蔬价格指数的变化情况:
记


当

(1)比较2012年上半年与下半年鲜蔬价格指数月平均值的大小(不要求计算过程);
(2)直接写出从2012年2月到2013年1月的12个月中价格指数环比下降的月份. 若从这12个月中随机选择连续的两个月进行观察,求所选两个月的价格指数都环比下降的概率;
(3)由图判断从哪个月开始连续三个月的价格指数方差最大. (结论不要求证明)
正确答案
见解析
解析
(1)上半年的鲜疏价格的月平均值大于下半年的鲜疏价格的月平均值.-----4分
(2)从2012年2月到2013年1月的12个月中价格指数环比下降的月份有
4月、5月、6月、9月、10月. ----------------------6分
设“所选两个月的价格指数均环比下降”为事件A, ------------------7分
在这12个月份中任取连续两个月共有11种不同的取法,--------------------------8分
其中事件A有(4月,5月),(5月,6月),(9月,10月),共3种情况. ------9分
∴
(3)从2012年11月开始,2012年11月,12月,2013年1月这连续3个月的价格指数方差最大。
--------------------------------13分
知识点
高三某班有学生56人,现将所有同学随机编号,用系统抽样的方法,抽取一个容量为4的样本,已知5号、33号、47号学生在样本中,则样本中还有一个学生的编号为
正确答案
解析
略
知识点
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元,根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示,经销商为下一个销售季度购进了130 t该农产品,以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润。
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率。
正确答案
(1) 
解析
(1)当X∈[100,130)时,T=500X-300(130-X)=800X-39 000.
当X∈[130,150]时,T=500×130=65 000.
所以
(2)由(1)知利润T不少于57 000元当且仅当120≤X≤150.
由直方图知需求量X∈[120,150]的频率为0.7,所以下一个销售季度内的利润T不少于57 000元的概率的估计值为0.7
知识点
某个年级有男生560人,女生420人,用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本,则此样本中男生人数为__________。
正确答案
160
解析
根据分层抽样的特点,此样本中男生人数为
知识点
已知圆O的半径为1,PA,PB为该圆的两条切线,A,B为两切点,那么
正确答案
解析
略
知识点
已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组,现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.
(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
(2)分别统计这10名学生的数学成绩,获得成绩数据的茎叶图如图4所示,求该样本的方差;
(3)在(2)的条件下,从这10名学生中随机抽取两名成绩不低于73分的学生,求被抽取到的两名学生的成绩之和不小于154分的概率。
正确答案
见解析。
解析
(1)由题意,得抽出号码为22的组数为3.
因为2+10×(3-1)=22,所以第1组抽出的号码应该为02,抽出的10名学生的号码依次分别为:02, 12, 22, 32, 42,52,62,72,82,92.
(2)这10名学生的平均成绩为:

故样本方差为:
(3)从这10名学生中随机抽取两名成绩不低于73分的学生,共有如下10种不同的取法:
(73,76),(73,78),(73,79),(73,81),(76,78),(76,79),(76,81),(78,79),(78,81),(79,81).
其中成绩之和不小于154分的有如下7种:(73,81),(76,78),(76,79),(76,81),(78,79),(78,81),(79,81).
故被抽取到的两名学生的成绩之和不小于154分的概率为:
知识点
某工厂的某种型号的机器的使用年限

根据上表可得回归方程
正确答案
12.38
解析
略
知识点
某班共有52人,现根据学生的学号,用系统抽样的方法,抽取一个容量为4的样本,已知3号、29号、42号同学在样本中,那么样本中还有一个同学的学号是
正确答案
解析
因为29号、42号的号码差为13,所以
知识点
扫码查看完整答案与解析