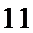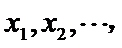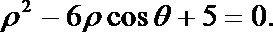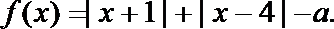- 统计与统计案例
- 共590题
12.已知样本数据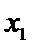
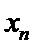
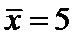
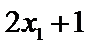
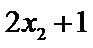

正确答案
解析
试题分析:因为样本数据 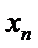
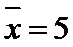
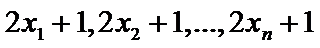
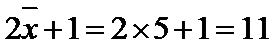
考查方向
解题思路
样本数据作线性变化后,其均值也作相应的线性变化。
易错点
不知道均值性质。
知识点
选做题:请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题计分.
22.选修4—1:几何证明选讲
如图,已知

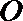

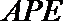
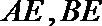
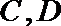
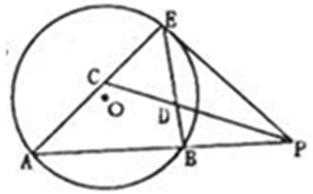
求证:
(1)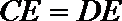
(2)
23.选修4—4:坐标系与参数方程
在直角坐标系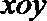
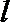
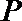
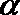
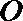
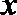
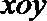
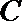
(1)若直线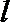
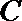
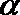
(2)设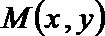
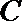
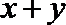
24.选修4—5:不等式选讲
设函数
(1)当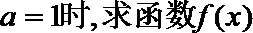
(2)若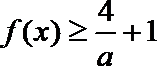
正确答案
22.

23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
6.为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息。设定原信息为a0a1a2,ai∈{0,1}(i=0,1,2),传输信息为h0a0a1a2h1h2,其中h0=a0⊕a1,h1=h0⊕a2,h2=h1⊕h0,⊕为运算规则为:0⊕0=0,0⊕1=1,1⊕0=1,1⊕1=0,例如原信息为111,则传输信息为011111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.气象意义上从春季进入夏季的标志为:“连续5天的日平均温度均不低于22 (℃)”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区有( )
正确答案
解析
甲地:5个数据的中位数为24,众数为22,根据数据得出:甲地连续5天的日平均温度记录数据可能为:22,22,24,25,26,其连续5天的日平均温度均不低于22;乙地:5个数据的中位数为27,总体均值为24,当5个数据为19,20,27,27,27可知其连续5天的日平均温度有低于22,故不正确;丙地:5个数据中有一个数据是32,总体均值为26,若有低于22,则取21,此时方差超出了10.8,可知其连续5天的日平均温度均不低于22.则肯定进入夏季的地区有甲、丙两地,故选择C选项。
考查方向
解题思路
利用相关概念逐一进行判断。
易错点
相关概念不熟悉导致出错。
知识点
用正偶数按下表排列
则2006在第几行第几列( )
正确答案
解析
解:每行用去4个偶数,而2006是第2006÷2=1003个偶数
又1003÷4=250…余3,
前250行共用去250×4=1000个偶数,剩下的3个偶数放入251行,
考虑到奇数行所排数从左到右由小到大,且前空一格,
∴2006在251行,第4列。
知识点
某高校在2012年的自主招生考试成绩中随机抽以100名学生的笔试成绩,按成绩分组,依次为第一组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185),统计后得到如图所示的频率分布直方图。
(1)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮大幅度,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(2)在(1)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被A考官面试的概率?
正确答案
见解析。
解析
(1)由图得,第3组的频率为0.06×5=0.3,故频数为30。
第4组的频率为0.04×5=0.2,故频数为20。
第5组的频率为0.02×5=0.1,故频数为10。
因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组分别为:
第3组:


所以,第3、4、5组每组各抽取3、2、1名学生进入第二轮面试。
(2)设第3组的3为同学为1,2,3.第4组的2位同学为a,b,第5组的1位同学为c。
则从6位同学中抽2位同学有15种可能,如下:
(1,2),(1,3),(1,a),(1,b),(1,c),(2,3),(2,a),(2,b),(2,c),(3,a),
(3,b),(3,c),(a,b),(a,c),(b,c)。
其中第4组的两位同学至少有1位同学入选的有:(1,a),(1,b),(2,a),(2,b),(2,c),(3,a),(3,b),(3,c),(a,b)9种可能。
所以第4组至少有一名学生被A考官面试的概率为
知识点
中国式过马路,是网友对部分中国人集体闯红灯现象的一种调侃,即,“凑够一撮人就可以走了,和红绿灯无关。我校对全校学生过马路方式进行调查,在所有参与调查的人中, “跟从别人闯红灯”“从不闯红灯”“带头闯红灯”人数如表所示:
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知“跟从别人闯红灯”的人中抽取45人,求n值;
(2)在“带头闯红灯”的人中,将男生的200人编号为001,002,…,200;将女生的300人编号为201,202,…,500,用系统抽样的方法抽取4人参加”文明交通”宣传活动,若抽取的第一个人的编号为100,把抽取的4人看成一个总体,从这4人中任选取2人,求这两人均女生的概率;
正确答案
解析
(1)由题意,得
(2)由系统抽样得的号码分别为100,225,350,475,
其中100号为男生,设为A1,而225,350,475都为女生,分别设为B1,B2,B3
从这4人中任选取2人所有的基本事件为
(A1,B1),(A1,B2),(A1,B3),(B1,B2),(B1,B3),(B2,B3),共有6个
这两人均女生的基本事件为
(B1,B2),(B1,B3),(B2,B3)共有3个
所以所求事件的概率
知识点
对人们的休闲方式的一次调查中,共调查了100人,其中女性60人,男性40人,女性中有38人主要的休闲方式是看电视,另外22人主要的休闲方式是运动;男性中有15人主要的休闲方式是看电视,另外25人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2列联表;
(2)判断性别与休闲方式是否有关。
参考公式: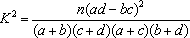
参考数据:60×40×53×47=5978400,620×620=384400, 384400÷59784≈6.4298.
正确答案
见解析。
解析
(1)2×2列联表如下:
(2)假设“休闲方式与性别无关”。
由表中数据计算得,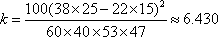
因为k≥5.024,所以有理由认为假设“休闲方式与性别无关”是不合理的,即有97.5%的把握认为“休闲方式与性别有关”,
知识点
为了解某校高三毕业

(1)求该校报考体育专业学生的总人数n;
(2)已知A、a是该校报考体育专业的两名学生,A的体重小于55千克, a的体重不小于






正确答案
见解析
解析
解:(1)由图知第四组的频率为
第五组的频率为.
又有条件知前三组的频率分别为
(2)易知按分层抽样抽取6名体重小于55千克和不小于70千克的学生中,体重小于55千克的学生4人,记为
体重不小于70千克的学生2人,记为
从中抽取满足条件的所有结果有:

所求事件的概率为
知识点
近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重。大气污染可引起心悸、呼吸困难等心肺疾病。为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
(1)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?
(2)在上述抽取的6人中选2人,求恰有一名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量
下面的临界值表供参考:
(参考公式

正确答案
见解析。
解析
(1)在患心肺疾病人群中抽6人,则抽取比例为
∴男性应该抽取
(2)在上述抽取的6名患者中, 女性的有2人,男性4人。女性2人记
























故上述抽取的6人中选2人,恰有一名女性的概率概率为
(3)∵

那么,我们有的把握认为是否患心肺疾病是与性别有关系的。 ……….10分
低碳生活,节能减排,控制污染源,控制排放,(回答基本正确就得分) ………12分
知识点
扫码查看完整答案与解析