- 统计与统计案例
- 共590题
6.从甲、乙等5名学生中随机选出2人,则甲被选中的概率为
正确答案
解析
设5个人分别为a b c d e
(a , b) (a , c) (a , d) (a , e) (b , c) (b , d) (b , e) (c , d) (c , e) (d , e)
含a的情况有: (a , b) (a , c) (a , d) (a , e) 所以a被选中的概率为:
考查方向
解题思路
分析题中所有情况的种数,以及含a的种数,利用古典概型的概率公式进行计算
易错点
分清该题为取球问题的一起取情况
知识点
8.某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则
正确答案
解析
由题意得立定跳远决赛的有8人,所以序号为1,2,3,4,5,6,7,8的学生入选,又因为同时进入立定跳远决赛和30秒跳绳决赛的有6人,所以30秒跳绳决赛的6人一定从1~8学号的学生选取,假设5号不入选,那么1~8序号的学生中有5人入选,与题意6人入选矛盾,所以5号一定入选。
考查方向
解题思路
把成绩由高到低排列,分析入选情况
易错点
分清9.10一定不入选,再假设分析前8个入选情况
知识点
某市民用水拟实行阶梯水价,每人用水量中不超过w立方米的部分按4元/立方米收费,超出w立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
19.如果w为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,w至少定为多少?
20.假设同组中的每个数据用该组区间的右端点值代替,当w=3时,估计该市居民该月的人均水费.
正确答案
由用水量的频率分布直方图知,
该市居民该月用水量在区间




率依次为




所以该月用水量不超过



依题意,

考查方向
解题思路
利用频率分布直方图与平均数的知识计算
易错点
该题平均水费的运算量有些大,计算要细心
正确答案
由用水量的频率分布直方图及题意,得居民该月用水费用的数据分组与频率分布表:
组号
1
2
3
4
5
6
7
8
分组
频率
根据题意,该市居民该月的人均水费估计为:

考查方向
解题思路
利用频率分布直方图与平均数的知识计算
易错点
该题平均水费的运算量有些大,计算要细心
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
甲、乙两套设备生产的同类型产品共4800件,采用分层抽样的方法从中抽取一个容量为80的样本进行质量检测,若样本中有50件产品由甲设备生产,则乙设备生产的产品总数为 件。
正确答案
1800
解析
∵样本容量为80,∴抽取的比例为

又样本中有50件产品由甲设备生产,∴样本中30件产品由乙设备生产,
∴乙设备生产的产品总数为30×60=1800。
知识点
一支田径运动队有男运动员56人,女运动员42人,现用分层抽样的方法抽取若干人,若抽取的男运动员有8人,则抽取的女运动员有______人。
正确答案
6
解析
设抽取的女运动员有x人,由题意可得,
知识点
海关对同时从A,B,C三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如右表所示. 工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
(1)求这6件样品中来自A,B,C各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
正确答案
见解析
解析
(1)因为工作人员是按分层抽样抽取商品,所以各地区抽取商品比例为:
所以各地区抽取商品数为:


(2)设各地区商品分别为:
基本时间空间

样本时间空间为:
所以这两件商品来自同一地区的概率为:
知识点
某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名。现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为
正确答案
解析
由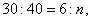
知识点
某网站针对“2014年法定节假日调休安排”展开的问卷调查,提出了A、B、C三种放假方案,调查结果如下:
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持A方案”的人中抽取了6人,求n的值;
(2)在“支持B方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率。
正确答案
(1)n=40
(2)
解析
(1)根据分层抽样按比例抽取,所以
解得
(2)35岁以下:
35岁以上:
设:将35岁以下4人标记为1、2、3、4,35岁以上1人标记为a.所有基本事件为:
其中满足条件得有

答:恰好有1个人在35岁以上(含35岁)的概率为
知识点
扫码查看完整答案与解析