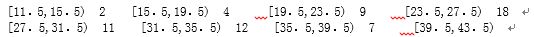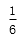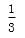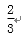统计与统计案例_章节学习

1

题型：单选题

|

单选题 · 5 分

有一个容量为66的样本，数据的分组及各组的频数如下：

根据样本的频率分布估计，数据落在[31.5,43.5)的概率约是(　　)

A

B

C

D

正确答案

B

解析

知识点

频率分布表用样本的数字特征估计总体的数字特征

1

题型：单选题

|

单选题 · 5 分

有一个容量为66的样本，数据的分组及各组的频数如下：

根据样本的频率分布估计，大于或等于31.5的数据约占(　　)

A

B

C

D

正确答案

B

解析

知识点

频率分布表用样本的数字特征估计总体的数字特征

1

题型：简答题

|

简答题 · 12 分

某校高三年级一次数学考试之后,为了解学生的数学学习情况, 随机抽取名学生的数

学成绩, 制成表所示的频率分布表。

(1) 求，，的值;

(2) 若从第三, 四, 五组中用分层抽样方法抽取6名学生，并在这6名学生中随机抽取2

名与张老师面谈，求第三组中至少有名学生与张老师面谈的概率。

正确答案

见解析。

解析

(1) 解：依题意，得，

解得，，，.

(2) 解：因为第三、四、五组共有60名学生，用分层抽样方法抽取6名学生，

则第三、四、五组分别抽取名，名，名.

第三组的名学生记为，第四组的名学生记为，第五组的名学生记为，

则从名学生中随机抽取名，共有种不同取法，具体如下：，，，，，，，，，

，，，，，.

其中第三组的名学生没有一名学生被抽取的情况共有种，具体如下：，，.

故第三组中至少有名学生与张老师面谈的概率为.

知识点

互斥事件、对立事件的概率分层抽样方法频率分布表

1

题型：填空题

|

填空题 · 5 分

某公司为了了解员工们的健康状况，随机抽取了部分员工作为样本，测量他们的体重（单位：公斤），体重的分组区间为[50,55），[55,60），[60,65），[65,70），[70,75]，由此得到样本的频率分布直方图，如图4所示，根据频率分布直方图，估计该公司员工体重的众数是_________；从这部分员工中随机抽取1位员工，则该员工的体重在[65,75]的概率是_________。

正确答案

解析

众数是，∵各分组频率分别为0.15，0.25，0.3，0.2，0.1，∴该员工的体重在[65,75]的概率是。

知识点

频率分布表

1

题型：简答题

|

简答题 · 12 分

某校高三（1）班共有名学生，他们每天自主学习的时间全部在分钟到分钟之间，按他们学习时间的长短分个组统计,得到如下频率分布表：

（1）求分布表中，的值；

（2）王老师为完成一项研究，按学习时间用分层抽样的方法从这名学生中抽取名进行研究，问应抽取多少名第一组的学生？

（3）已知第一组学生中男、女生人数相同，在（2）的条件下抽取的第一组学生中，既有男生又有女生的概率是多少？

正确答案

见解析。

解析

（1），，

（2）设应抽取名第一组的学生，则得。

故应抽取2名第一组的学生，

（3）在（2）的条件下应抽取2名第一组的学生，记第一组中2名男生为，2名女生为。

按时间用分层抽样的方法抽取2名第一组的学生共有种结果，列举如下：

，

其中既有男生又有女生被抽中的有这4种结果，

所以既有男生又有女生被抽中的概率为.

知识点

古典概型的概率分层抽样方法频率分布表

1

题型：填空题

|

填空题 · 5 分

从某项综合能力测试中抽取50人的成绩，统计如表，则这50人成绩的平均数等于 ▲ 、方差为 ▲ .

正确答案

3;

解析

知识点

频率分布表

1

题型：简答题

|

简答题 · 13 分

某市电视台为了宣传举办问答活动，随机对该市15～65岁的人群抽样了n人，回答问题统计结果如下图表所示：

（1）分别求出a，b，x，y的值；

（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，则第2，3，4组每组各抽取多少人?

（3）在（2）的前提下，电视台决定在所抽取的6人中随机抽取2人颁发幸运奖，求所抽取的人中第2组至少有1人获得幸运奖的概率。

正确答案

见解析。

解析

（1）由频率表中第1组数据可知，第1组总人数为，

再结合频率分布直方图可知.

∴a=100×0.020×10×0.9=18，

b=100×0.025×10×0.36=9，

,

（2）第2，3，4组中回答正确的共有54人。

∴利用分层抽样在54人中抽取6人，每组分别抽取的人数为：

第2组：人,

第3组：人,

第4组：人。

（3）设第2组的2人为、，第3组的3人为、、，第4组的1人为，则从6人中抽2人所有可能的结果有：，，，，，，，，，，，，，，，共15个基本事件，

其中第2组至少有1人被抽中的有，，，，，，，，这9个基本事件。

∴第2组至少有1人获得幸运奖的概率为

知识点

古典概型的概率分层抽样方法频率分布表频率分布直方图

1

题型：简答题

|

简答题 · 12 分

某单位名员工参加“社区低碳你我他”活动，他们

的年龄在25岁至50岁之间，按年龄分组：第1组

，第2组，第3组，第4组

，第5组，得到的频率分布直方图

如图5所示，下表是年龄的频率分布表。

（1）求正整数，，的值；

（2）现要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，则年龄在第1，2，3组的人数分别是多少？

（3）在（2）的条件下，从这6人中随机抽取2人参加社区宣传交流活动，求恰有1人在第3组的概率。

正确答案

见解析。

解析

解：（1）由频率分布直方图可知，与两组的人数相同，

所以人，

且人。

总人数人，

（2）因为第1，2，3组共有25+25+100=150人，利用分层抽样在150名员工中抽取人，每组抽取的人数分别为：

第1组的人数为，

第2组的人数为，

第3组的人数为，

所以第1，2，3组分别抽取1人，1人，4人，

（3）由（2）可设第1组的1人为，第2组的1人为，第3组的4人分别为，则从6人中抽取2人的所有可能结果为：

，，，，，，，，，，，，，，，共有种，

其中恰有1人年龄在第3组的所有结果为：

，，，，，，，，共有8种。

所以恰有1人年龄在第3组的概率为，

知识点

古典概型的概率频率分布表频率分布直方图

1

题型：简答题

|

简答题 · 12 分

某校高三（1）班共有名学生，他们每天自主学习的时间全部在分钟到分钟之间，按他们学习时间的长短分个组统计,得到如下频率分布表：

（1）求分布表中，的值；

（2）王老师为完成一项研究，按学习时间用分层抽样的方法从这名学生中抽取名进行研究，问应抽取多少名第一组的学生？

（3）已知第一组学生中男、女生人数相同，在（2）的条件下抽取的第一组学生中，既有男生又有女生的概率是多少？

正确答案

见解析。

解析

（1），，

（2）设应抽取名第一组的学生，则得。

故应抽取2名第一组的学生，

（3）在（2）的条件下应抽取2名第一组的学生，记第一组中2名男生为，2名女生为。

按时间用分层抽样的方法抽取2名第一组的学生共有种结果，列举如下：

，

其中既有男生又有女生被抽中的有这4种结果，

所以既有男生又有女生被抽中的概率为.

知识点

古典概型的概率分层抽样方法频率分布表

1

题型：简答题

|

简答题 · 12 分

某中学高三实验班的一次数学测试成绩的茎叶图(图3)和频率分布直方图(图4)都受到不同程度的破坏，可见部分如下图所示，据此解答如下问题。

（1）求全班人数及分数在之间的频数；

（2）计算频率分布直方图中的矩形的高；

（3）若要从分数在[80，100]之间的试卷中任取两份分析学生的答题情况，在抽取的试卷中，求至少有一份分数在[90，100]之间的概率。

正确答案

见解析。

解析

（1）由茎叶图可知，分数在之间的频数为2,频率为，所以全班人数为（人）故分数在之间的频数为.

(2) 分数在之间的频数为4, 频率为

所以频率分布直方图中的矩形的高为

（3）用表示之间的4个分数，用表示之间的2个分数，则满足条件的所有基本事件为：，，，，共15个，

其中满足条件的基本事件有：

，，共9个

所以至少有一份分数在[90，100]之间的概率为.

知识点

频率分布表

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点