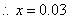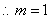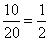- 统计与统计案例
- 共590题
一次考试中,五名学生的数学、物理成绩如下表所示:
(1)要从5学生中选2人参加一项活动,求选中的学生中至少有一人的
物理成绩高于90分的概率;
(2)请在所给的直角坐标系中画出它们的散点图,并求这些数据的线性回归方程
正确答案
见解析。
解析
(1)从












其中至少有一人物理成绩高于








故上述抽取的



(2)散点图如右所示.
可求得:










故


知识点
某高校在2012年的自主招生考试成绩中随机抽以100名学生的

(1)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进

(2)在(1)的前提下,学校决定在

正确答案
见解析。
解析
(1)
由图得,第3组的频率为0.3,故频数为30,第四组的频率为0.2,故频数为20,第5组的频率为0.1,故频数为10。因为第3,4,5组共有60组学生,所以利用分层抽样在60组学生中抽取6名学生,每组分别为
(2)
知识点
根据某固定测速点测得的某时段内过往的100辆机
动车的行驶速度(单位:km/h)绘制的频率分布直方图如
图(3)所示,该路段限速标志牌提示机动车辆正常行驶速
度为60 km/h~120 km/h,则该时段内过往的这100辆机
动车中属非正常行驶的有 辆,图中的x值为 。
正确答案
15、0.0175
解析
知识点
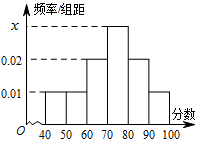
某学校对学生的考试成绩作抽样调查,得到成绩的频率分布直方图如图所示,其中[70,80)对应的数值被污损,记为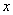
(1)求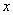
(2)记[90,100]为A组,[80,90)为B组,[70,80)为C组,用分层抽样的办法从[90,100],[80,90),[70,80)三个分数段的学生中抽出6人参加比赛,从中任选3人为正选队员,求正选队员中有A组学生的概率。
正确答案
见解析。
解析
(1)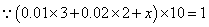
(2)设从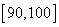
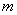
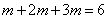
记从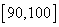
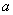
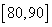
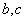
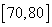
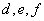
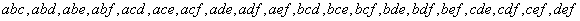
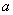
知识点
随机抽取100名学生,测得他们的身高(单位





正确答案

解析
略
知识点
某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量,若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”,若小区内有至少
(1)求所选的两个小区恰有一个为“非低碳小区”的概率;
(2)假定选择的“非低碳小区”为小区


正确答案
(1)
(2)三个月后小区
解析
(1)设三个“非低碳小区”为
用

则从5个小区中任选两个小区,所有可能的结果有10个,它们是









用

是:





故所求概率为
(2)由图1可知月碳排放量不超过
由图2可知,三个月后的低碳族的比例为
所以三个月后小区
知识点
为了解本市的交通状况,某校高一年级的同学分成了甲、乙、丙三个组,从下午13点到18点,分别对三个路口的机动车通行情况进行了实际调查,并绘制了频率分布直方图(如图),记甲、乙、丙三个组所调查数据的标准差分别为

正确答案
解析
略
知识点
如图,三行三列的方阵中有9个数

正确答案
解析
略
知识点
如图是根据某城市部分居民2012年月平均用水量(单位:吨)绘制的样本频率分布直方图,样本数据的分组为[1,2),[2,3),[3,4),……,[6,7],已知样本中月均用水量低于4吨的户数为102,则样本中月均用水量不低于4吨的户数为
正确答案
解析
略
知识点
某高校在2012年的自主招生考试成绩中随机抽以100名学生的笔试成绩,按成绩分组,依次为第一组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185),统计后得到如图所示的频率分布直方图。
(1)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮大幅度,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(2)在(1)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被A考官面试的概率?
正确答案
见解析。
解析
(1)由图得,第3组的频率为0.06×5=0.3,故频数为30。
第4组的频率为0.04×5=0.2,故频数为20。
第5组的频率为0.02×5=0.1,故频数为10。
因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组分别为:
第3组:


所以,第3、4、5组每组各抽取3、2、1名学生进入第二轮面试。
(2)设第3组的3为同学为1,2,3.第4组的2位同学为a,b,第5组的1位同学为c。
则从6位同学中抽2位同学有15种可能,如下:
(1,2),(1,3),(1,a),(1,b),(1,c),(2,3),(2,a),(2,b),(2,c),(3,a),
(3,b),(3,c),(a,b),(a,c),(b,c)。
其中第4组的两位同学至少有1位同学入选的有:(1,a),(1,b),(2,a),(2,b),(2,c),(3,a),(3,b),(3,c),(a,b)9种可能。
所以第4组至少有一名学生被A考官面试的概率为
知识点
扫码查看完整答案与解析