- 统计与统计案例
- 共590题
对某校高三年级学生参加社区服务次数进行统计,随机抽取

(1)求出表中

(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
正确答案
见解析
解析
(1)由分组



所以
因为频数之和为



因为


(2)因为该校高三学生有240人,分组

所以估计该校高三学生参加社区服务的次数在此区间内的人数为
(3)这个样本参加社区服务的次数不少于20次的学生共有
设在区间



则任选


而两人都在

所以所求概率为

知识点
在某一届江西省中学生运动会上,承办学校招募了8名男志愿者和12名女志愿者。定义身高在180cm以上(包括180cm)为“高个子”,身高在180cm以下(不包括180cm)为“非高个子”。现将这20名志愿者的身高编成如下茎叶图(精确到lcm),由于污染导致这个茎叶图中的一个数据模糊。
(1)如果用分层抽样的方法以“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)在女志愿者身高的中位数是175的条件下,求茎叶图中,这个模糊数据所表示的身高不大于172的概率。
正确答案
见解析
解析
解:(1)根据茎叶图,有“高个子”8人,“非高个子”12人,
用分层抽样的方法,每个人被抽中的概率是
所以选中的“高个子”有
“ 非高个子”有
从这五个人A,B,C,D,E中选出两个人共有:
(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E)
共有十种不同方法;
其中至少有一人是“高个子”的选法有:
(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),共有七种. -
因此,至少有一人是“高个子”的概率是
(2)设看不清的女志愿者身高为
满足女志愿者身高的中位数是17

其中不大于172的
所以在女志愿者身高的中位数是175条件下,这个模糊数据表示的身高不大于172的概率是
知识点
某市高三数学抽样考试中,对



正确答案
810
解析
解析:根据直方图,组距为





因为


人数为



为
知识点
为检查国家全民健身运动的落实情况,在某社区成年居民中随机抽取200名,统计其平均每天参加体育活动时间(

正确答案
960
解析

知识点
对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(1)求出表中M,p及图中a的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[25,30)内的概率。
正确答案
见解析。
解析
(1)由分组[10,15)内的频数是10,频率是0.25知,
∴M=40。
∵频数之和为40,
∴10+24+m+2=40,m=4.
∵a是对应分组[15,20)的频率与组距的商,
∴
(2)因为该校高三学生有240人,分组[10,15)内的频率是0.25,
∴估计该校高三学生参加社区服务的次数在此区间内的人数为60人。
(3)这个样本参加社区服务的次数不少于20次的学生共有m+2=6人,
设在区间[20,25)内的人为a1,a2,a3,a4,在区间[25,30)内的人为b1,b2。
则任选2人共有(a1,a2),(a1,a3),(a1,a4),(a1,b1),(a1,b2),(a2,a3),(a2,a4),(a2,b1),(a2,b2),(a3,a4),(a3,b1),(a3,b2),(a4,b1),(a4,b2),(b1,b2)15种情况,而两人都在[25,30)内只能是(b1,b2)一种,
∴所求概率为
知识点
对某校高一年级学生参加社区服务次数进行统计,随机抽取


(1)求出表中M、p及图中a的值;
(2)若该校高一学生有360人,试估计他们参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[20,25)内的概率。
正确答案
(1)M=40,a=0.125,p=0.075
(2)225
(3)
解析
(1)由题可知



又 



则

(2)参加在社区服务次数在区间

(3)在样本中,处于








知识点
14.下图茎叶图是甲.乙两人在5次综合测评中成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为()
正确答案
解析
由图可知,甲的5次成绩分别是88.89.90.91.92,易知甲的平均分为90.乙的成绩分别是83.83.87.99,其中被污损的那次成绩为90到99中的某一个.设被污损的那次成绩为





知识点
21.对某校高三年级学生参加社区服务次数进行统计,随机抽取

根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(Ⅰ)求出表中

(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
正确答案
见解析。
解析
(Ⅰ)由分组

因为频数之和为


因为

(Ⅱ)因为该校高三学生有240人,分组

所以估计该校高三学生参加社区服务的次数在此区间内的人数为
(Ⅲ)这个样本参加社区服务的次数不少于20次的学生共有










知识点
3.如图是某体育比赛现场上七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
正确答案
解析
略。
知识点
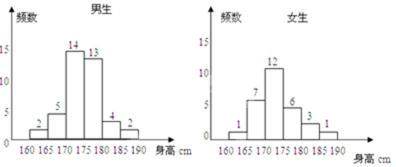
18.为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3) 从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析