- 统计与统计案例
- 共590题
如图所示茎叶图记录了甲、乙两组各
正确答案
76;82.8
解析
略
知识点
某年级举行校园歌曲演唱比赛,七位评委为学生甲打出的演唱分数茎叶图如下图所示,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为 , ,
正确答案
85 ; 3.2
解析
去掉最高分93和最低分79后,剩下的分数分别为83,84,86,84,88,平均数为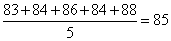
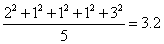
知识点
据相关调查数据统计,2010年某大城市私家车平均每天增加400辆,除此之外,公
交车等公共车辆也增长过快,造成交通拥堵现象日益严重,现有A、B、C三辆车从同
一地点同时出发,开往甲、乙、丙三地,已知A、B、C这三辆车在驶往目的地的过程
中,出现堵车的概率

(1)求这三辆车恰有两辆车被堵的概率;
(2)求这三辆车至少有两辆车不被堵的概率。
正确答案
见解析。
解析
(1)设”这三辆车恰有两辆车被堵”的事件为A。
所以
(2)设“这三辆车至少有两辆车不被堵”的事件为

这三辆车没有一辆车被堵的概率为

所以
即这三辆车至少有两辆车不被堵的概率为
知识点
为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h),试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5 2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4 1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(1)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(2)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
正确答案
见解析
解析
(1)设A药观测数据的平均数为

由观测结果可得




由以上计算结果可得

(2)由观测结果可绘制如下茎叶图:
从以上茎叶图可以看出,A药疗效的试验结果有

知识点
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售。如果当天卖不完,剩下的玫瑰花做垃圾处理。
(1)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式。
(2)花店记录了100天
(i)假设花店在这100天内每天购进17枝玫瑰花,求这100天
(ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率。
正确答案
(1)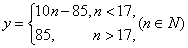
解析
(1)当日需求量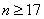
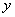
当日需求量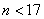
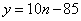
∴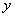
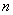
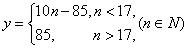
(2)(i)这100天中有10天的日利润为55元,20天的日利润为65元,16天的日利润为75元,54天的日利润为85元,所以这100天的平均利润为
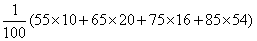
(ii)利润不低于75元当且仅当日需求不少于16枝,故当天的利润不少于75元的概率为
知识点
据相关调查数据统计,2012年某大城市私家车平均每天增加400辆,除此之外,公交车等公共车辆也增长过快,造成交通拥堵现象日益严重,现有A、B、C三辆车从同一地点同时出发,开往甲、乙、丙三地,已知A、B、C这三辆车在驶往目的地的过程中,出现堵车的概率

(1)求这三辆车恰有两辆车被堵的概率;
(2)用


正确答案
见解析。
解析
(1)设”这三辆车恰有两辆车被堵”的事件为A。
所以
(2)依题意得
计算得


故
故
知识点
某公司有男职员45名,女职员15名,按照分层抽样的方法组建了一个4人的科研攻关小组。
(1)求某职员被抽到的概率及科研攻关小组中男、女职员的人数;
(2)经过一个月的学习、讨论,这个科研攻关组决定选出两名职员做某项实验,方法是先从小组里选出1名职员做实验,该职员做完后,再从小组内剩下的职员中选一名做实验,求选出的两名职员中恰有一名女职员的概率;
(3)试验结束后,第一次做试验的职员得到的试验数据为68,70,71,72,74,第二次做试验的职员得到的试验数据为69,70,70,72,74,请问哪位职员的实验更稳定?并说明理由。
正确答案
见解析。
解析
(1)

设有



(2)把







(3)

第二次做试验的职员做的实验更稳定………………………12分
知识点
在某大学自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级. 某考场考生的两科考试成绩的数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.
(1)求该考场考生中“阅读与表达”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分,求该考场考生“数学与逻辑”科目的平均分;
(3)已知参加本考场测试的考生中,恰有两人的两科成绩均为A. 在至少一科成绩为A的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为A的概率。
正确答案
(1)3
(2)2.9
(3)
解析
(1)因为“数学与逻辑”科目中成绩等级为B的考生有10人,
所以该考场有
所以该考场考生中“阅读与表达”科目中成绩等级为A的人数为
(2)求该考场考生“数学与逻辑”科目的平均分为

(3)因为两科考试中,共有6人得分等级为A,又恰有两人的两科成绩等级均为A,
所以还有2人只有一个科目得分为A………………9分
设这四人为甲,乙,丙,丁,其中甲,乙是两科成绩都是A的同学,则在至少一科成绩等级为A的考生中,随机抽取两人进行访谈,基本事件空间为


设“随机抽取两人进行访谈,这两人的两科成绩等级均为A”为事件B,所以事件B中包含的基本事件有1个,则
知识点
为了解某校学生的视力情况,现采用随机抽样的方式从该校的












(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?
(2)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)
(3)根据数据推断


正确答案
(1)A班学生的视力较好
(2)B班5名学生视力的方差较大
(3)16
解析
(1)解:A班5名学生的视力平均数为
B班5名学生的视力平均数为
从数据结果来看A班学生的视力较好. ……………… 4分
(2)解:B班5名学生视力的方差较大. ……………… 8分
(3)解:在A班抽取的5名学生中,视力大于4.6的有2名,
所以这5名学生视力大于4.6的频率为
所以全班40名学生中视力大于4.6的大约有
则根据数据可推断A班有16名学生视力大于4.6. ……………… 13分
知识点
甲、乙两种水稻试验品种连续5年的单位面积平均产量如下(单位:t/hm2),根据这组数据下列说法正确的是
正确答案
解析
略
知识点
扫码查看完整答案与解析