- 统计与统计案例
- 共590题
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图,甲班学生身高的众数与乙班学生中位数之差为_________
正确答案
3.5
解析
略
知识点
某校高三学生体检后,为了解高三学生的视力情况,该校从高三六个班的300名学生中以班为单位(每班学生50人),每班按随机抽样抽取了8名学生的视力数据,其中高三(1)班抽取的8名学生的视力数据与人数见下表:
(1)用上述样本数据估计高三(1)班学生视力的平均值;
(2)已知其余五个班学生视力的平均值分别为





正确答案
见解析。
解析
(1)高三文科(1)班抽取的8名学生视力的平均值为

据此估计高三文科(1)班学生视力的平均值约为
(2)因为高三文科六个班学生视力的平均值分别为





所以任意抽取两个文科班学生视力的平均值数对有














其中抽取的两个班学生视力的平均值之差的绝对值不小于










所以抽取的两个班学生视力的平均值之差的绝对值不小于

知识点
若把能表示为两个连续偶数的平方差的正整数称为“和平数”,则在1~100这100个数中,能称为“和平数”的所有数的和是
正确答案
解析
设两个连续偶数为



知识点
某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如左表所示。已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16.
(1)求
(2) 现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查,问应在第三批次中抽取教职工多少名?
(3) 已知
正确答案
见解析。
解析
(1)由

(2)第三批次的人数为
设应在第三批次中抽取

∴应在第三批次中抽取12名。
(3)设第三批次中女教职工比男教职工多的事件为A,第三批次女教职工和男教职工数记为数对


而事件A包含的基本事件有
知识点
某车间在两天内,每天生产10件某产品,其中第一天、第二天分别生产出了1件、2件次品.而质检部门每天要从生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过。
(1)求第一天产品通过检查的概率;
(2)若厂内对车间生产的产品采用记分制:两天全不通过检查得0分;通过1天、2天分别得1分、2分.求该车间这两天的所得分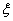
(3)求两天全部通过的概率。
正确答案
见解析。
解析
(1)∵随意抽取4件产品检查是随机事件,而第一天有9件正品。
∴第一天通过检查的概率为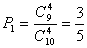
(2)第二天通过检查的概率为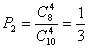
两天的所得分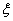
∵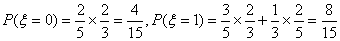
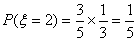
∴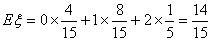
(3)同(1),第二天通过检查的概率为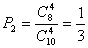
因第一、第二天是否通过检查相互独立,
所以,两天全部通过检查的概率为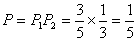
知识点
在一次射击训练中,一小组的成绩如下表:
已知该小组的平均成绩为8.1环,那么成绩为8环的人数是( )。
正确答案
解析
设成绩为8环的人数是
知识点
已知图1、图2分别表示A、B两城市某月1日至6日当天最低气温的数据折线图(其中横轴




正确答案
解析
略
知识点
吴同学晨练所花时间(单位:分钟)分别为x,y,30,29,31,已知这组数据的平均数为30,方差为2,则|x-y|的值为
正确答案
解析
略
知识点
《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在+20—80mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属于碎酒驾车,某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾驶员共20人,检测结果如下表:
(1)求检测数据中醉酒驾驶的频率;
(2)估计检测数据中酒精含量的平均数。
正确答案
见解析
解析
(1)所求频率为
(2)估计所求平均数为

知识点
在黄冈市青年歌手大赛中,七位评委为某选手打出的分数如下:91 89 91 96 94 95 94
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
正确答案
解析
略
知识点
扫码查看完整答案与解析













