- 统计与统计案例
- 共590题
5.已知一组数据a,b,9,10,11的平均数为10,方差为2,则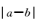
正确答案
解析
由题意可得a+b=20,(a-10)2+(b-10)2=8,解得a=8,b=12或a=12,b=8.故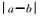
知识点
15.已知总体的各值由小到大依次为2,3,3,7,a,b,12,13.7,18.3,20,且总体的中位数为10.5。若要使该总体的方差最小,则a,b的取值分别是________
正确答案
10.5 10.5
解析
这10个数的中位数为
要使总体方差最小,即要(a-10)2+(b-10)2最小,即a2+b2-20(a+b)+200最小,
∵a>0,b>0,∴a2+b2≥
又a+b=21,∴当a=b=10.5时,方差取得最小值。
知识点
5.已知一组数据a,b,9,10,11的平均数为10,方差为2,则
正确答案
解析
由题意可得a+b=20,(a-10)2+(b-10)2=8,解得a=8,b=12或a=12,b=8.故
知识点
15.已知总体的各值由小到大依次为2,3,3,7,a,b,12,13.7,18.3,20,且总体的中位数为10.5.若要使该总体的方差最小,则a,b的取值分别是________
正确答案
10.5 10.5
解析
这10个数的中位数为
要使总体方差最小,即要(a-10)2+(b-10)2最小,即a2+b2-20(a+b)+200最小,
∵a>0,b>0,∴a2+b2≥
又a+b=21,∴当a=b=10.5时,方差取得最小值。
知识点
9.如图所示的茎叶图表示甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 某车间将10名技工平均分为甲,乙两组加工某种零件,在单位时间内每个技工加工零件若 干,其中合格零件的个数如下表:
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此分析两组技工的
(2)质检部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车

正确答案
(1)依据题中的数据可得,
X甲=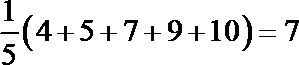
X乙=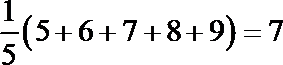
所以两组技工的总体水平相同,甲组中技工的技术水平差异比乙组大。
(2)设事件A表示:该车间“质量合格”,则从甲、乙两组中各抽取1名技工完成合格零件个数的基本事件为:(4,5)(4,6)(4,7)(4,8)(4,9)(5,5)(5,6)(5,7)(5,8)(5,9)(7,5)(7,6)(7,7)(7,8)(7,9)(9,5)(9,6)(9,7)(9,8)(9,9)(10,5)(10,6)(10,7)(10,8)(10,9)共25种,所以概率P(A)= 17/25
解析
利用平均数和方差公式,求得甲的平均数是7,乙的平均数是7,甲的方差为5.2,乙的方差为2,两组技工的总体水平相同,甲组中技工的技术水平差异比乙组大;列出所有时间发生的基本事件,共17种,所以质量合格的概率为17/25
考查方向
本题主要考查平均数与方差的求法。考查随机事件发生的概率
解题思路
按照概念依次求解
易错点
对平均数和方差理解不透彻,不会计算随机事件发生的概率
知识点
18.某校对高一年级学生寒假参加社区服务的次数进行了统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
(Ⅰ)求表中n, p的值和频率分布直方图中
(Ⅱ)如果用分层抽样的方法从样本服务次数在[10,15)和[25,30)的人中共抽取6人,再从这6人中选2人,求2人服务次数都在[10,15)的概率.
正确答案
见解析
解析
(Ⅰ)
因20÷



中位数位于区间
则0.125x=0.25,所以x=2,所以学生参加社区服务次数的中位数为17次。
(Ⅱ)
由题意知样本服务次数在[10,15)有20人,样本服务次数在[25,30)有4人. 如果用分层抽样的方法从样本服务次数在[10,15)和[25,30)的人中共抽取6人,则抽取的服务次数在[10,15)和[25,30)的人数分别为:

记服务次数在[10,15)为

从已抽取的6人中任选两人的所有可能为:
共15种.设“2人服务次数都在[10,15)”为事件

共10种,
所以
考查方向
解题思路
根据表和图的信息,仔细求解
易错点
作图,遗漏数据
知识点
4.已知变量x与y正相关,且由观测数据算得样本平均数x=3,y=3.5,则由该观测数据算得的线性回归方程可能是( )
正确答案
解析
∵变量x与y正相关,∴可以排除A,D;因为回归直线方程恒过样本中心点样本将平均数x=3,y=3.5,代入,C符合,B不符合,故选:C
考查方向
解题思路
变量x与y正相关,所以x前边的系数为正,再利用回归直线方程恒过样本中心点是关键。
易错点
1、本题易在判断x,y的正负相关关系上出错 。
2、本题不容易搞清楚样本平均数与线性回归方程的关系。
知识点
3.已知数据



正确答案
解析
数据增加一个联系实际可知500超出体重,所以平均数会增加,50个数据的中位数可能为中间第25,26两个数(数值相等),所以增加一个最大数后,中位数变为第26个,不发生变化,所以选B
考查方向
解题思路
【解题思路】本题属于简单题,可使用直接法,
易错点
数据结合实际,忽视中位数的定义
知识点
6.气象意义上从春季进入夏季的标志为:“连续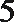
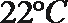
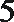
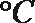
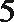
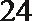
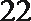
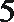
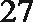
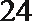
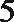
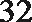
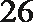
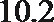
正确答案
解析
①中至少有两个整数22,故后面两个数大于24,②中易举反例19,20,27,27,27。③中设另外四个数分别为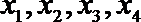
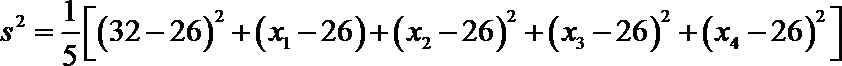
考查方向
本题主要考查大概三视图及几何体的表面积知识
解题思路
对每组数据分别分析。
易错点
1、特征数的概念不清。
2、分析处理数据的能力不强。
知识点
扫码查看完整答案与解析
















