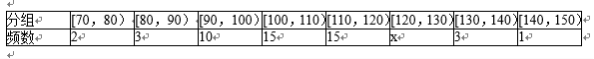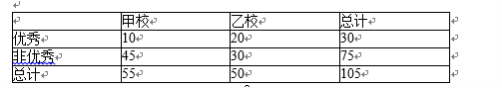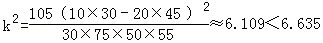- 统计与统计案例
- 共590题
某课题组进行城市空气质量调查,按地域把24个城市分成甲、乙、丙三组,对应城市数分别为4、12、8,若用分层抽样抽取6个城市,则甲组中应抽取的城市数为____。
正确答案
1
解析
略
知识点
为了让学生更多地了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛,了为解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请根据频率分布表,解答下列问题:
(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(2)为鼓励更的学生了解“数学史”知识,成绩不低于85分的同学能获奖,请估计在参加的800名学生中大概有多少同学获奖.
(3)在上述统计数据的分析中有一项计算,见算法流程图,求输出S的值.
正确答案
见解析。
解析
知识点
一个学校高三年级共有学生600人,其中男生有360人,女生有240人,为了调查高三学生的复习状况,用分层抽样的方法从全体高三学生中抽取一个容量为50的样本,应抽取女生 人。
正确答案
20
解析

知识点
从8名女生,4名男生选出6名学生组成课外小组,如果按性别比例分层抽样,则不同的抽取方法种数( )
正确答案
解析
解:根据题意,从8名女生,4名男生中按性别比例分层抽样选出6名学生,
需要抽出男生6×
需要抽出女生6×
则共有C84×C42种抽取方法,
知识点
某学校三个兴趣小组的学

学校要对这三个小组的活动效果进行抽样调查,按小组分层抽样的方法,从参加这三个兴趣小组的学生中抽取30人,结果篮球组被抽出12人,则
正确答案
30
解析
略
知识点
某地共有


正确答案
解析
略
知识点
某学校高一、高二、高三年级的学生人数之比为
正确答案
解析
略
知识点
某市甲、乙两校高二级学生分别有1100人和1000人,为了解两校全体高二级学生期末统考的数学成绩情况,采用分层抽样方法从这两所学校共抽取105名高二学生的数学成绩,并得到成绩频数分布表如下,规定考试成绩在[120,150]为优秀。
甲校:
乙校:
(1)求表中x与y的值;
(2)由以上统计数据完成下面2x2列联表,问是否有99%的把握认为学生数学成绩优秀与所在学校有关?
正确答案
见解析
解析
(1)由分层抽样可知,甲校抽取105×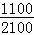
所以x=55﹣(2+3+10+15+15+3+1)=6,y=50﹣(1+2+9+8+10+10+3)=7;
(2)2x2列联表如下
所以
所以没有99%的把握认为学生数学成绩优秀与所在学校有关。
知识点
某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成
五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在90分以上(含90分)的学生为“优秀”,成绩小于90分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格。
(1)求“优秀”和“良好”学生的人数;
(2)如果用分层抽样的方法从“优秀”和“良好”的学生中选出10人,求“优秀”和“良好”的学生分别选出几人?
(3)若甲是在(2)选出的“优秀”学生中的一个,则从选出的“优秀”学生中再选2人参加某专项测试,求甲被选中的概
率是多少?
正确答案
见解析
解析
(1)依题意良好学生的人数为40×(0.01+0.07+0.06)×5=28人,
优秀学生的人数为40×(0.04+0.02)×5=12人。
(2)优秀与良好的人数比为3:7,所以采用分层抽样的方法抽取的10人中有优秀3人,良好7人。
(3)将(2)选出的优秀的三名学生记为甲,乙,丙,则从这3人中任选2人的所有基本事件包括:甲乙,甲丙,乙丙共3个基本事件,
其中含甲的基本事件为甲乙,甲丙2个,
所以甲被选中的概率是
知识点
某中学共有学生2000人,各年级男,女生人数如下表:
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19。
(1)现用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?
(2)已知y≥245,z≥245,求高三年级中女生比男生多的概率。
正确答案
见解析
解析
解:(1)∵
高三年级人数为y+z=2000﹣(373+377+380+370)=500
现用分层抽样的方法在全校抽取48名学生,
应在高三年级抽取的人数为
(2)设高三年级女生比男生多的事件为A,高三年级女生,
男生数记为(y,z),由(2)知y+z=500,且y,z∈N,
基本事件空间包含的基本事件有(245,255),(246,254),(247,253),┅,(255,245)共11个。
事件A包含的基本事件(251,249),(252,248),(253,247),(254,246),(255,245)共5个。
∴
知识点
扫码查看完整答案与解析