热门试卷

19．近年空气质量逐步恶化，雾霾天气现象出现增多，大气污染危害加重，大气污染可引起心悸，呼吸困难等心肺疾病，为了解某市心肺疾病是否与性别有关，在某医院随机对入院50人进行了问卷调查，得到了如下的列联表.

（Ⅰ）用分层抽样的方法在患心肺疾病的人群中抽6人，其中男性抽多少人？

（Ⅱ）在上述抽取的6人中选2人，求恰有一名女性的概率；

（Ⅲ）为了研究心肺疾病是否与性别有关，请计算出统计量，并回答有多大把握认为心肺疾病与性别有关？

下面的临界值表供参考：

18.某班优秀生16人，中等生24人，学困生8人，现采用分层抽样的方法从这些学生中抽取6名学生做学习习惯调查，

（Ⅰ）求应从优秀生、中等生、学困生中分别抽取的学生人数；

（Ⅱ）若从抽取的6名学生中随机抽取2名学生做进一步数据分析，

        （1）列出所有可能的抽取结果；

        （2）求抽取的2名学生均为中等生的概率.

17．成都海关对同时从A，B，C三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量(单位：件)如表所示．工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测．

（1）求这6件样品中来自A，B，C各地区商品的数量；

（2）若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．

18．中国式过马路，是网友对部分中国人集体闯红灯现象的一种调侃，即，“凑够一撮人就可以走了，和红绿灯无关”。某校对全校学生过马路方式进行调查，在所有参与调查的人中， “跟从别人闯红灯”“从不闯红灯”“带头闯红灯”人数如表所示：

（1）在所有参与调查的人中，用分层抽样的方法抽取个人，已知“跟从别人闯红灯”的人中抽取50人，求的值；

（2）在“带头闯红灯”的人中，将男生的200人编号为001，002，…，200；将女生的200人编号为201，202，…，400，用系统抽样的方法抽取5人参加“文明交通”宣传活动，若抽取的第一个人的编号为30，把抽取的5人看成一个总体，从这5人中任选取2人，求至少有一名女生的概率。

某校学生会进行了一次关于“消防安全”的调查活动，组织部分学生干部在几个大型小区随机抽取了50名居民进行问卷调查，活动结束后，团委会对问卷结果进行了统计，并将其中“是否知道灭火器使用方法（知道或不知道）”的调查结果统计如下表：

（1）求上表中的m、n的值，并补全右图所示的的频率直方图；

（2）在被调查的居民中，若从年龄在[10,20)，[20,30)的居民中各随机选取1人参加消防知识讲座，求选中的两人中仅有一人不知道灭火器的使用方法的概率。

19．某学校为了了解高三学生的身体健康状况，在该校高三年级学生中随机抽取了100名学生进行调查，按日睡眠时间（单位：小时）分组得到如图1的频率分布表和如图2的频率分布直方图。

（Ⅰ）请补全频率分布直方图，并求频率分布表中的a，b；

（Ⅱ）现用分层抽样法从第一、二、五组中抽取6名学生进行体检，求第一、二、五组各应抽取多少名学生？

（III）在上述6名学生中随机抽取2名学生进行某专项体检，求这2名学生中恰有一名学生在第二组的概率。

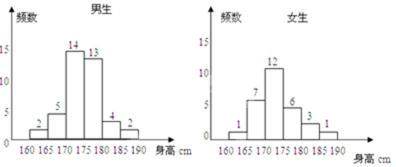
18．为了解学生身高情况，某校以10%的比例对全校700名学生按性别进行分层抽样调查，测得身高情况的统计图如下：

（1）估计该校男生的人数；

（2）估计该校学生身高在170～185cm之间的概率；

（3） 从样本中身高在180～190cm之间的男生中任选2人，求至少有1人身高在185～190cm之间的概率。