- 统计与统计案例
- 共590题
4.以下四个命题:其中真命题为( )
①从匀速传递的产品生产流水线上,质检员每20分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量相关性越强,则相关系数的绝对值越接近于1;
③在回归直线方程
④对分类变量X与Y,它们的随机变量K2的观测值k来说,k越小,“X与Y有关系”的把握程度越大.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.某中学高二年级的一个研究性学习小组拟完成下列两项调查:
①从某社区430户高收入家庭,980户中等收入家庭,290户低收入家庭中任意选出170户调查社会购买力的某项指标;
②从本年级12名体育特长生中随机选出5人调查其学习负担情况;
则该研究性学习小组宜采用的抽样方法分别是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.某地为了调查职业满意度,决定用分层抽样的方法从公务员、教师、自由职业者三个群体的相关人员中抽取若干人组成调查小组,相关数据见下表:
则调查小组的总人数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.某地为了调查职业满意度,决定用分层抽样的方法从公务员、教师、自由职业者三个群体的相关人员中抽取若干人组成调查小组,相关数据见下表:
则调查小组的总人数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
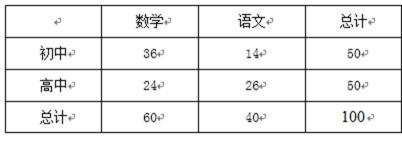
18.某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了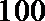
(Ⅰ) 用分层抽样的方法从喜欢数学的学生中随机抽取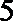
(Ⅱ) 在(Ⅰ)中抽取的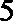
正确答案
(Ⅰ) 由表中数据可知, 高中学生应该抽取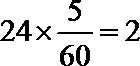
(Ⅱ) 记抽取的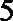
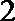
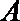
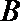
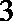

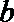
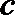
则从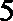
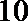
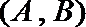
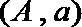
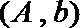
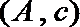
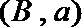
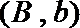
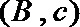
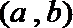
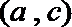
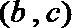
其中恰有1名高中学生的情况有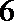
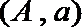
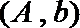
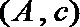
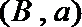
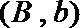
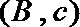
故所求概率为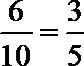
解析
解析已在路上飞奔,马上就到!
知识点
6.某学院的








正确答案
40
解析
解析已在路上飞奔,马上就到!
知识点
17.某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,数学成绩如下表所示:
(I)为了了解同学们前段复习的得失,以便制定下阶段的复习计划,学校将采用分层抽样的方法抽取100名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,求他被抽中的概率;
(II)已知本次数学成绩的优秀线为110分,试根据所提供数据估计该中学达到优秀线的人数;
(III)作出频率分布直方图,并估计该学校本次考试的数学平均分.(同一组中的数据用该组区间的中点值作代表)
正确答案
解:(I)分层抽样中,每个个体被抽到的概率均为
故甲同学被抽到的概率
(II)由题意
故估计该中学达到优秀线的人数
(III)频率分布直方图.
该学校本次考试数学平均分

估计该学校本次考试的数学平均分为90分.
解析
解析已在路上飞奔,马上就到!
知识点
20.一工厂生产甲, 乙, 丙三种样式的杯子,每种样式均有500ml和700ml两种型号,某天的产量如右表(单位:个):按样式分层抽样的方法在这个月生产的杯子中抽取100个,其中有甲样式杯子25个.
(1)求z的值;
(2)用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,从这个样本中任取2个杯子,求至少有1个500ml杯子的概率.
正确答案
解: (1).设该厂本月生产的乙样式的杯子为n个,在丙样式的杯子中抽取x个,由题意得,

则100-40-25=35,
所以
(2)设所抽样本中有m个500ml杯子,
因为用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,
所以
也就是抽取了2个500ml杯子,3个700ml杯子,
分别记作S1,S2;B1,B2,B3,则从中任取2个的所有基本事件为
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)
共10个,其中至少有1个500ml杯子的基本事件有7个基本事件:
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),
所以从中任取2个至少有1个500ml杯子的概率为
解析
解析已在路上飞奔,马上就到!
知识点
1.一个学校的教师具有高级职称的人数为160,具有中级职称的人数为320,具有初级职称的人数为200,其余人员人数为80。采用分层抽样的方法,从中抽取38人作为职工代表参加教代会。则从上述各层中依次抽取的人数分别是( )
正确答案
解析
教师总人数为160+320+200+80=760,因为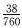
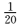
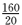
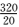
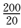
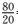
知识点
1.一个学校的教师具有高级职称的人数为160,具有中级职称的人数为320,具有初级职称的人数为200,其余人员人数为80.采用分层抽样的方法,从中抽取38人作为职工代表参加教代会.则从上述各层中依次抽取的人数分别是( )
正确答案
解析
教师总人数为160+320+200+80=760,因为





知识点
扫码查看完整答案与解析