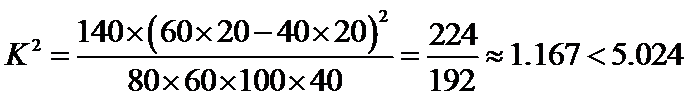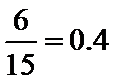统计与统计案例_章节学习

1

题型：单选题

|

单选题 · 5 分

3.根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图,以下结论中不正确的是（）

A逐年比较,2008年减少二氧化碳排放量的效果最显著

B2007年我国治理二氧化碳排放显现成效

C2006年以来我国二氧化碳年排放量呈减少趋势

D2006年以来我国二氧化碳年排放量与年份正相关

正确答案

D

解析

由柱形图可知2006年以来,我国二氧化碳排放量基本成递减趋势,所以二氧化碳排放量与年份负相关,故选D.

考查方向

本题主要考查统计知识及对学生柱形图的理解

解题思路

本题把统计知识与时下的热点环保问题巧妙地结合在一起,该题背景比较新颖,设问比较灵活,是一道考查考生能力的好题.解答此题的关键是学生能从图中读出有用的信息,再根据得到的信息正确作出判断.

易错点

图像的变化增减趋势

知识点

分层抽样方法

1

题型：填空题

|

填空题 · 5 分

5．某校高一年级有学生人，高二年级有学生人，现采用分层抽样的方法从全校学生中抽出人，其中从高一年级学生中抽出人，则从高三年级学生中抽取的人数为 ________.

正确答案

解析

根据题意设出高一和高三要抽取的人数，根据题意列出关于所设的未知量的方程，解出结果，根据高一的总人数和要抽取的人数，求出每个个体被抽到的概率，根据概率相等做出高三的总人数．

由题意得：高一年级与高二年级的抽取比例为：400:360，即10:9，故高二年级抽取人数为18人，所以高三年级抽取的人数为55-20-18=17人

所以答案为

考查方向

本题主要考查了分层抽样,是统计部分的高频考点，体现了学生的基础知识掌握能力。

解题思路

按照分层抽样的定义，按照一定地比例抽样，抓住一定比例即可快速解决问题。

易错点

不能理清分层抽样中的比例问题。

知识点

分层抽样方法

1

题型：单选题

|

单选题 · 5 分

3.某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异，拟从这三个年级中按人数比例抽取部分学生进行调查，则最合理的抽样方法是( )

A抽签法

B系统抽样法

C分层抽样法

D随机数法

正确答案

C

解析

按照各种抽样方法的适用范围可知，应使用分层抽样.故选C选项

考查方向

本题主要考察抽样方法的适用范围等知识，意在考察考生的应用基础知识的能力。

解题思路

直接根据抽样方法的适用范围即可得到答案。

易错点

不清楚各类抽样方法的适用范围导致出错。

知识点

分层抽样方法

1

题型：填空题

|

填空题 · 5 分

12.随机抽取100名年龄在…，年龄段的市民进行问卷调查，由此得到样本的频率分布直方图如图所示，从不小于30岁的人中按年龄段分层抽样的方法随机抽取22人，则在年龄段抽取的人数为 ▲ .

正确答案

2

解析

根据频率分布直方图可知

考查方向

本题考察频率分布直方图，分层抽样方法，比较简单

解题思路

本题的解题思路

1）根据小矩形面积对应为频率，计算不小于30岁的频率，与之间的频率。

2）计算两部分的比例

3）使用分层抽样的性质计算人数

易错点

本题易于在分层抽样的性质上出错

知识点

分层抽样方法频率分布直方图

1

题型：单选题

|

单选题 · 5 分

6.2016年3月9日至15日，谷歌人工智能系统“阿尔法”迎战围棋冠军李世石，最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类的胜利，也有许多人持反对意见，有网友为此进行了调查，在参加调查的2548名男性中有1560名持反对意见，　2452名女性中有1200名持反对意见，在运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时，应采用的统计方法是

A茎叶图

B分层抽样

C独立性检验

D回归直线方程

正确答案

C

解析

通过对题意的理解运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系，只有独立性检验可以说明性别与判断“人机大战是人类的胜利”是否有关系，有多大的把握认为他们有关，所以选C选项.

考查方向

本题主要考查统计的知识，独立性检验.

解题思路

1.观察答案给的几种情况，分析本题应采用哪一种.

易错点

本题学生们如果对统计中的一些知识点不熟悉的话，可能会选错.

知识点

分层抽样方法系统抽样方法茎叶图

1

题型：简答题

|

简答题 · 12 分

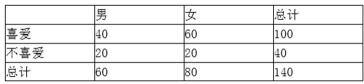
周立波是海派清口创始人和《壹周·立波秀》节目的主持人，他的点评视角独特，语言幽默犀利，给观众留下了深刻的印象．某机构为了了解观众对《壹周·立波秀》节目的喜爱程度，随机调查了观看了该节目的140名观众，得到如下的列联表：（单位：名）

19.从这60名男观众中按对《壹周·立波秀》节目是否喜爱采取分层抽样，抽取一个容量为6的样本，问样本中喜爱与不喜爱的观众各有多少名？

20，根据以上列联表，问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱《壹周·立波秀》节目有关．（精确到0.001）

21.从19题中的6名男性观众中随机选取两名作跟踪调查，求选到的两名观众都喜爱《壹周·立波秀》节目的概率．

第(1)小题正确答案及相关解析

正确答案

喜爱的观众有4名；不喜爱的观众有2名．

解析

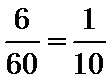
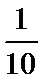
抽样比为，则样本中喜爱的观众有40×=4名；不喜爱的观众有6﹣4=2名．

考查方向

分层抽样的统计方法

解题思路

直接计算抽样比，即可算出喜爱与不喜爱的人数；

易错点

对“独立性检验的思想”不理解易出错

第(2)小题正确答案及相关解析

正确答案

不能在犯错误的概率不超过0．025的前提下认为观众性别与喜爱有关．

解析

假设：观众性别与喜爱无关，由已知数据可求得，

∴ 不能在犯错误的概率不超过0．025的前提下认为观众性别与喜爱有关．

考查方向

独立性检验的思想及其初步应用.

解题思路

直接代入公式计算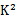,通过表中数据得出相应结论

易错点

对“独立性检验的思想”不理解易出错

第(3)小题正确答案及相关解析

正确答案

0.4

解析

记喜爱的4名男性观众为a，b，c，d，不喜爱的2名男性观众为1，2；则基本事件分别为：（a，b），（a，c），（a，d），（a，1），（a，2），（b，c），（b，d），（b，1），（b，2），（c，d），（c，1），（c，2），（d，1），（d，2），（1，2）．

其中选到的两名观众都喜爱的事件有6个，

故其概率为P（A）=

考查方向

等可能事件的概率

解题思路

直接列出总事件及发生事件的情况，直接求比。

易错点

对“独立性检验的思想”不理解易出错

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：简答题

|

简答题 · 16 分

已知椭圆（常数），点是上的动点，是右顶点，定点的坐标为。

（1）若与重合，求的焦点坐标；

（2）若，求的最大值与最小值；

（3）若的最小值为，求的取值范围。

正确答案

见解析。

解析

（1），椭圆方程为，

∴ 左、右焦点坐标为。

（2），椭圆方程为，设，则

∴ 时；时。

（3）设动点，则

∵ 当时，取最小值，且，∴ 且

解得。

知识点

收集数据的方法

1

题型：简答题

|

简答题 · 12 分

17．某城市户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图

（1）求直方图中的值；

（2）求月平均用电量的众数和中位数；

（3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？

正确答案

（1）由（0.002+0.0095+0.011+0.0125+x+0.005+0.0025）×20=1

得：X=0.0075，所以直方图中X的值是0.0075

（2）月平均用电量的众数是

因为，所以月平均用电量的中位数在内，设中位数为，由得：，所以月平均用电量的中位数是

（3）月平均用电量为的用户有户，月平均用电量为的用户有户，月平均用电量为的用户有户，月平均用电量为的用户有户，抽取比例，所以月平均用电量在的用户中应抽取户

解析

解析已在路上飞奔，马上就到！

知识点

分层抽样方法频率分布直方图众数、中位数、平均数

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

正确答案

正确答案

解析

知识点

正确答案

解析

知识点