- 动能 动能定理
- 共113题
如图,MN为铝质薄平板,铝板上方和下方分别有垂直于图平面的匀强磁场(未画出)。一带电粒子从紧贴铝板上表面的P点垂直于铝板向上射出,从Q点穿越铝板后到达PQ的中点O。已知粒子穿越铝板时,其动能损失一半,速度方向和电荷量不变。不计重力。铝板上方和下方的磁感应强度大小之比为 ( )
正确答案
解析
略
知识点
下列关于功和机械能的说法,正确的是( )
正确答案
解析
重力势能的减少量等于重力对物体所作的功,与有无阻力作用无关,A错;由动能定理可知,合力对物体所做的功等于物体动能的变化量,B正确;物体的重力势能是物体与地球相互作用能,势能大小与零势能点的选取有关,C正确;在只有重力做功的前提下才可满足物体动能的减少量等于物体重力势能的增加量,D错。
知识点
如图为质量相等的两个质点A、B在同一直线上运动的v﹣t图象,由图可知( )
正确答案
解析
解:A、两质点位移等于图线与时间轴包围的面积,显然B的位移较大,因而A错误;B、速度时间图象反映的是质点任意时刻的速度情况,两个图象的交点表明该时刻速度相等,故B正确;C、两质点位移等于图线与时间轴包围的面积,显然B的位移较大,因而C正确;D、两质点质量相等,t=0时刻动能均为0,t时刻速度相等,因而动能也相等,根据动能定理,可以知道,合外力做的功相等;
故选BCD。
知识点
动能相等的两人造地球卫星A、B的轨道半径之比RA:RB= 1:2,它们的角速度之比
正确答案

解析
两卫星绕地球做匀速圆周运动,其万有引力充当向心力,


知识点
如图,两根相距l=0.4m、电阻不计的平行光滑金属导轨水平放置,一端与阻值R=0.15Ω的电阻相连。导轨x>0一侧存在沿x方向均匀增大的稳恒磁场,其方向与导轨平面垂直,变化率k=0.5T/m,x=0处磁场的磁感应强度B0=0.5T。一根质量m=0.1kg、电阻r=0.05Ω的金属棒置于导轨上,并与导轨垂直。棒在外力作用下从x=0处以初速度v0=2m/s沿导轨向右运动,运动过程中电阻上消耗的功率不变。
求:
(1)同路中的电流;
(2)金属棒在x=2m处的速度;
(3)金属棒从x=0运动到x=2m过程中安培力做功的大小;
(4)金属棒从x=0运动到x=2m过程中外力的平均功率。
正确答案
见解析。
解析
(1)电阻消耗功率不变所以
所以
(2)因为I相等所以
(3)由

(4)根据动能定理,
又
所以
知识点
如图,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经过3.0s罗到斜坡上的A点。已知O点是斜坡的起点,斜坡与水平面的夹角
(1) A点与O点时的速度大小;
(2) 运动员离开0点时的速度大小;
(3) 运动员落到A点时的动能。
正确答案
见解析
解析
(1)运动员在竖直方向做自由落体运动,有
A点与O点的距离
(2)设运动员离开O点的速度为
即
解得
(3)由机械能守恒,取A点位重力势能零点,运动员落到A点的动能为
知识点
质量为m的小球从空中O点以速度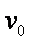
正确答案
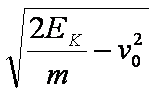
解析
略
知识点
一探险队员在探险时遇到一山沟,山沟的一侧竖直,另一侧的坡面呈抛物线形状,此队员从山沟的竖直一侧,以速度v0沿水平方向跳向另一侧坡面,如图所示,以沟底的O点为原点建立坐标系Oxy,已知,山沟竖直一侧的高度为2h,坡面的抛物线方程为
(1)求此人落到坡面时的动能;
(2)此人水平跳出的速度为多大时,他落在坡面时的动能最小?动能的最小值为多少?
正确答案
(1)
(2)
解析
(1)设该队员在空中运动的时间为t,在坡面上落点的横坐标为x,纵坐标为y,由运动学公式和已知条件得
x=v0t①
2h-y=
根据题意有

由机械能守恒,落到坡面时的动能为


联立①②③④式得

(2)⑤式可以改写为

v2极小的条件为⑥式中的平方项等于0,由此得

此时v2=3gh,则最小动能为
(

知识点
质量是0.2kg的皮球以5m/s的水平速度与墙相碰再以3m/s的速度反弹回来,设初速度方向为正,皮球动量变化量为 kg. m/s,动能变化量为 J。
正确答案
-1.6 1.6
解析
略
知识点
如图为某高台滑雪轨道部分简化示意图。其中AB段是助滑雪道,倾角为







(1)从C点水平飞出时速度的大小;
(2)运动员在着陆雪道CD上的着陆位置与C点的距离;
(3)运动员滑过D点时的速度大小;
(4)滑雪运动员从A到D克服摩擦力做的功为多少。
正确答案
见解析
解析
(1) 滑雪运动员从A到C的过程中,由动能定理得:
mgh-μmgL=
解得vc=10m/s
(2)滑雪运动员从C水平飞出落到着陆雪道过程中做平抛运动,
x=vct… …① y=
得 t=1.5s x=15m
着陆点位置与C点的距离s= s=18.75m
着陆位置到D点的距离s’=DC-S=9.375m
(3) 滑雪运动员在着陆雪道上做匀加速直线运动
初速度为
加速度为mgsinθ-μmgcosθ=ma1
a1=4m/s2
运动到D点的速度为vD2-v02=2a1s’ …
vD=20m/s
(4)从A点到D点动能定理

Wf=4125J
知识点
扫码查看完整答案与解析