- 动能 动能定理
- 共113题
有一半径为R=0.4m的光滑半圆轨道，直径BC竖直，与粗糙水平面相切于B点，如图所示。在距B点s=2.1m的A点有一质量为m=0.2kg的小滑块，小滑块与水平面间的动摩擦因数μ = 0.5，在与水平方向成α=53º的恒力F的
24．小滑块运动到C点时速度的大小？
25．小滑块运动到圆轨道的B点，撤去F时受到轨道的支持力为多大？
26．恒力F的大小？
正确答案
解析
（1）在C点：
考查方向
考查物体做圆周运动向心力的分析，及其与速度的关系公式：
解题思路
分析物体在C点的受力，得出合外力，根据合外力提供向心力 
易错点
对向心力由什么力提供容易模糊不清。
正确答案
(2)12.5N
解析
（2）在从B到C的过程中，由机械能守恒定律可知
考查方向
考查根据动能动能定理求速度：
解题思路
根据B到C过程中动能定理的公式解得物体在B点的速度，根据速度与向心力、合外力
易错点
对向心力由什么力提供容易模糊不清。
正确答案
(3)2N
解析
在从A到B的过程中
考查方向
考查牛顿第二运动定律：F合力=ma。考查运动学的基本公式：
解题思路
对A到B的过程中使用动能定理解得恒力F的大小，或者根据运动学公式求出加速度a，再根据匀速运动的条件(受力平衡) 求解恒力F的大小。
易错点
对向心力由什么力提供容易模糊不清。
如图甲所示，M、N 为一对竖直放置的平行金属板，中心各有一小孔 P 和 Q，PQ 连线 垂直金属板，现有质量 m=2.0×10-27 kg，电荷量 q=1.6×10-19C 带正电的粒子连续不断地从 小孔 P 飘入 M、N 板之间，带电粒子在小孔 P 处的初速可忽略。在 M、N 间加有如图乙所 示的交变电压，且 t=0 时 M 板电势高于 N 板电势。带电粒子在 M、N 间运动过程中，粒子 所受重力以及粒子之间的相互作用力均可忽略不计。
28.如果两平行金属板间距离 d=5.0cm， 求：
①带电粒子从小孔 Q 中射出时的最大速度值；
② 在 t=0.125×10
29.如果在
正确答案
（1）①
解析
（1）带电粒子在电场中运动的加速度
①带电粒子经过半个周期加速运动，前进的距离
②在t=0．125×10-5s时刻飘入P孔的带电粒子，在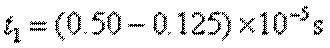
解得EkQ=5．0×10-20J
考查方向
解题思路
（1）进入到金属板之间的带电粒子的加速度根据牛顿第二定律和
结合求解．再由Vm=at即可求出最大速度。
易错点
此题很难，每个点都容易出错。
正确答案
（2）d＜2．5cm
解析
（2）如果只在[n~（n+0．25）]×10-5s内，
即在每个周期的
只要每个周期内
则在每个周期内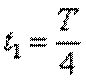
每个周期内
在
在
所以，
在每个周期内
在
并可从小孔Q中射出，
则两板间距离d应满足的条件是
解得 s =2．5cm 即两板间距离d应满足的条件是d＜2．5cm
考查方向
解题思路
（2）通过分析每个周期内带电粒子的运动情况，确定只有在每个周期的0～
时间内放出的带电粒子才能从小孔Q中射出时应满足的条件，根据牛顿第二定律和运动学公式求解各物理量之间应满足的关系．
易错点
此题很难，每个点都容易出错。
20.如图所示，可视为质点的质量为m且所带电量为q的小球，用一绝缘轻质细绳悬
A 小球在运动过程中机械能守恒
B小球在运动过程中机械能不守恒
C小球在运动过程的最小速度至少为
D小球在运动过程的最大速度至少为
正确答案
解析
因为在小球在运动过程中电场力做了功，所以机械能不守恒，故A错误，B正确；
小球在运动过程中电场力
考查方向
解题思路
1、根据机械能守恒定律的条件判定是否守恒。
2、找出电场力和重力的合力的大小方向，将电场和重力场等效，在等效场的最高点速度最小，根据动能定理求出最小速度。
易错点
本题的易错点就是以为在竖直最高点速度最小。
知识点
16．如图，电梯质量为M，地板上放置一个质量为m的物体，轻质钢索拉电梯由静止开始向上加速运动，当上升高度为H时，速度达到v，不计空气阻力，则
A钢索的拉力做功等于
B钢索对电梯及物体构成的系统做功等于
C地板对物体的支持力做功等于
D地板克服物体的重力做功的平均功率等于mgv
正确答案
解析
A选项，对电梯与物体整体使用动能定理有：W拉力－(M+m)gH=
W支持力=
考查方向
1、考查动能定理的基本公式。
2、整体法与隔离法分析物体运动。
3、功率的公式P=Fv。
解题思路
1、对电梯与物体进行整体分析，受重力和绳子拉力，拉力做正功，重力做负功，写出动能定理的表达式：W拉力－(M+m)gH=
2、单独分析物体受重力和地板对物体的支持力，支持力做正功，重力做负功，写出动能定理的表达式：
W支持力－mgH=
3、根据功率公式P=Fv分析平均功率。
易错点
1、误认为绳子拉力做功等于物体动能变化量。
2、运用动能定理时对物体受力分析不完全。
3、不理解克服重力做功的含义：即重力做负功。
知识点
如图所示，长 L=0.20m 的不可伸长的轻绳上端固定在 O 点， 下端系一质量 m=0.10kg 的小球（可视为质点），将绳拉至水平位 置，无初速地释放小球。当小球运动至 O 点正下方的 M 点时，绳 刚好被拉断。经过一段时间，小球落到了水平地面上 P 点，P 点 与 M 点的水平距离 x=0.80m，不计空气阻力，取重力加速度 g=10m/s2。求：
23.小球运动至 M 点时的速率 v；
24.M 点距水平地面的高度 h。
25.绳所能承受的最大拉力 F 的大小；
正确答案
(1)2．0
解析
（1）小球自绳处于水平位置释放到最低点的过程机械能守恒，则有mgL=
考查方向
抛体运动功能关系、机械能守恒定律及其应用牛顿运动定律、牛顿定律的应用
解题思路
（1）因为是曲线运动，所以对小球由机械能守恒或者动能定理列方程求解；
易错点
不应该出错
正确答案
0．8m
解析
设小球自M点到P点的运动时间为t，则h=
考查方向
解题思路
由平抛运动规律求解。
易错点
不应该出错
正确答案
3N
解析
设小球通过最低点时绳的拉力为F′，根据牛顿第二定律有
考查方向
抛体运动功能关系、机械能守恒定律及其应用牛顿运动定律、牛顿定律的应用
解题思路
在M点由合力提供向心力可求F；
易错点
不应该出错
扫码查看完整答案与解析