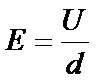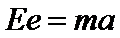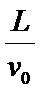- 带电粒子在匀强电场中的运动
- 共205题
21.正对着并水平放置的两平行金属板连接在如图电路中，板长为L，板间距为d，在距离板的右端 2L 处有一竖直放置的光屏 M。D为理想二极管（即正向电阻为0，反向电阻无穷大），R为滑动变阻器，R0为定值电阻。将滑片P置于滑动变阻器正中间，闭合电键S，让一带电量为q、质量为m的质点从两板左端连线的中点N以水平速度v0射入板间，质点未碰极板，最后垂直打在 M屏上。在保持电键S闭合的情况下，下列分析或结论正确的是( )
AA．质点在板间运动的过程中与它从板的右端运动到光屏的过程中速度变化相同
B板间电场强度大小为
C若仅将滑片P向下滑动一段后，再让该质点从N点以水平速度v0射入板间，质点依然会垂直打在光屏上
D若仅将两平行板的间距变大一些，再让该质点从N点以水平速度v0射入板间，质点依然会垂直打在光屏上
正确答案
解析
由题意知，粒子在板间做类平抛运动，要使最后垂直打在 M屏上，离开板间后竖直方向做减速运动，到达M板时竖直速度减为零，而水平方向一直做匀速运动，设离开板时竖直速度为vy，质点在板间运动的过程中速度变化为vy，从板的右端运动到光屏的过程中速度变化为- vy，故A错误；粒子从板的右端运动到光屏的过程中用时
考查方向
本题考查带电粒子在复合场中的运动
解题思路
不管是在单一场还是复合场，首先分析清楚带电粒子的受力情况，根据受力分析再来判断物体的运动情况。最再选择对应的物理规律。
易错点
带电粒子在复合场中的运动过程，以及受力情况分析不清楚。
知识点
25、如图所示，直径分别为D和2D的同心圆处于同一竖直面内，O为圆心，GH为大圆的水平直径。两圆之间的环形区域（Ⅰ区）和小圆内部（Ⅱ区）均存在垂直圆面向里的匀强磁场。间距为d的两平行金属极板间有一匀强电场，上极板开有一小孔。一质量为m，电量为+q的粒子由小孔下方d/2处静止释放，加速后粒子以竖直向上的速度v射出电场，由点紧靠大圆内侧射入磁场。不计粒子的重力。（1）求极板间电场强度的大小；（2）若粒子运动轨迹与小圆相切，求区磁感应强度的大小；（3）若Ⅰ区，Ⅱ区磁感应强度的大小分别为2mv/qD，4mv/qD，粒子运动一段时间后再次经过H点，求这段时间粒子运动的路程。
正确答案
见解析
解析
Ⅱ区域的磁感应强度为
设粒子在Ⅰ区和Ⅱ区做圆周运动的周期分别为T1、T2，由运动公式可得：
据题意分析，粒子两次与大圆相切的时间间隔内，运动轨迹如图所示，
根据对称性可知，Ⅰ区两段圆弧所对的圆心角相同，设为
由几何关系可得：
设粒子在Ⅰ区和Ⅱ区做圆周运动的时间分别为t1、t2，可得：
考查方向
带电粒子在电磁和磁场中的运动
解题思路
根据离子进入磁场的速度大小，准确分析离子的运动轨迹，以及对应的轨道半径是解决本题的关键
易错点
带电粒子在磁场中的运动的轨迹分析
知识点
求：（1）离子在电场中运动的时间t1；（2）P点距O点的距离y1和离子在磁场中运动的加速度大小a
正确答案
见解析
解析
（1）设离子垂直打到荧光屏上的M点时，
沿y方向的分速度大小为vy，在电场中运动的加速度为a1，
则：vy＝v0 /tan30o，由牛顿第二定律得：qE=ma1，
竖直分速度：vy=a1t1，解得：
（2）由几何关系可知：
解得：
设离子在磁场中做圆周运动半径为y2，则：y2cos30o＝v0t1，
而： 
考查方向
本题主要考查带电粒子在匀强磁场中的运动；带电粒子在匀强电场中的运动．
解题思路
（1）离子在电场中做类平抛运动，应用类平抛运动规律可以求出离子的运动时间．（2）作出离子运动轨迹，根据几何知识求出距离，由牛顿第二定律求出加速度．
易错点
本题考查了粒子在电场与磁场中的运动，分析清楚离子运动过程，作出粒子运动轨迹，应用类平抛运动规律、牛顿第二定律即可正确解题，解题时要注意几何知识的应用
知识点
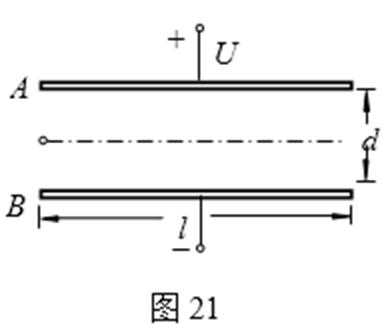
14．如图21所示，真空中有平行正对金属板A、B，它们分别接在输出电压恒为U=91V的电源两端，金属板长L＝10cm、两金属板间的距离d=3.2 cm， A、B两板间的电场可以视为匀强电场。现使一电子从两金属板左侧中间以v0=2.0×107m/s的速度垂直于电场方向进入电场，然后从两金属板右侧射出。已知电子的质量m=0.91×10-30kg，电荷量e=1.6×10-19C，两极板电场的边缘效应及电子所受的重力均可忽略不计。求：(计算结果保留两位有效数字)
（1）电子在电场中运动的加速度a的大小；
（2）电子射出电场时在沿电场线方向上的侧移量y；
（3）从电子进入电场到离开电场的过程中，其动量增量的大小。
正确答案
（1）a=5.0×1014m/s2
（2）y=0.63cm
（3）
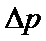
解析
（1）设金属板A、B间的电场强度为E，则
根据牛顿第二定律有：
解得：a=5.0×1014m/s2
（2）电子以速度v0进入金属板A、B间，在垂直于电场方向做匀速直线运动，沿电场方向做初速度为零的匀加速直线运动。
电子在电场中运动的时间为 t=
电子射出电场时在沿电场线方向的侧移量
解得：y=0.63cm
（3）设电子从进入电场到离开电场时间t=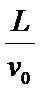
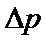
根据动量定理有：
解得：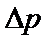
考查方向
解题思路
（1）根据牛顿第二定律求加速度。
（2）根据类平抛运动求偏转位移
（3）根据动量定理求动量
易错点
侧位移的求解，动量变化
知识点
9．如图所示，充电后的平行板电容器水平放置，上极板正中有一小孔。一带电小球从
正确答案
解析
1、由于场强方向和小球的电性都不知道，则无法确定场强方向和小球带何种电荷。
2、重力向下，小球做减速运动则电场力一定向上。
考查方向
解题思路
明确小球的受力情况和运动规律，结合动能定理列式分析场强方向。
易错点
小球的受力情况和运动规律
知识点
扫码查看完整答案与解析