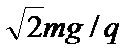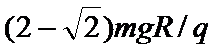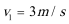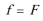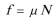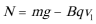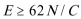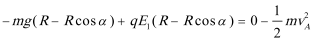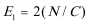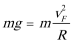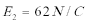- 带电粒子在匀强电场中的运动
- 共205题
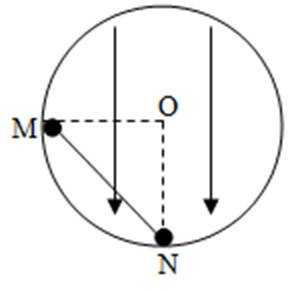
17.如图为一固定的内壁光滑.为R的绝缘圆筒的竖直截面，筒内有竖直向下的匀强电场，质量分别为3m和m的带正黾小球M.N，电量均为q ,两小球用绝缘轻杆相连并紧靠圆筒，不计两球间的静电力，开始时，M与圆心等高，N在筒的最低点，由静止释放后，两球始终在竖直平面内往复运动，且N球恰不会脱离轨道，重力加速度取g ,由此可以判断
AN球可以达圆筒的最高点
BN球增加的电势能总等于M球减少的电势能
C电场强度E的大小为
D同一时刻，两球所在位置的最大电势差为
正确答案
解析
A.从能量角度分析，若N能到达最高点，重力对其做负功，M的重力势能不变，整个系统重力做负功，同理得电场力也做负功，无其它力对系统做功，不满足能量守恒，则N不能到达最高点，故A错误;
B.在整个过程中，M、N沿电场方向的位移大小不一定相等，N球增加的电势能不一定等于M球减少的电势能，故B错误;
C、D.N球恰好不会脱离轨道，则此时杆恰好处于竖直位置，则此时NO两点连线与过O点的水平线的夹角为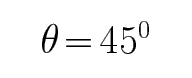
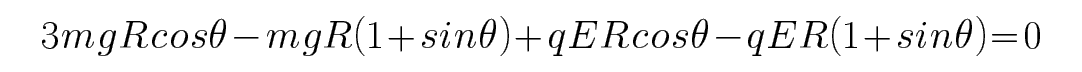
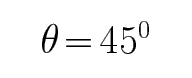
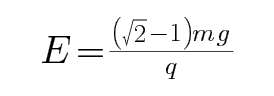
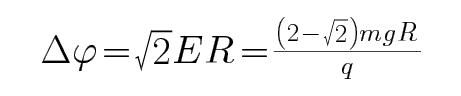
考查方向
功能关系；动能定理；带电粒子在匀强电场中的运动
解题思路
假定N能到最高点，用能量的角度分析是不可能的，对整个过程分析，两小球沿电场线方向的位移不一定是相等的；找出N球恰好不脱离轨道的位置，结合几何关系由动能定理解答.
易错点
关键理解能量的转化与守恒定律，假定N能达最高点由能量关系可分析出是不可能的.
教师点评
本题考查了带电粒子在匀强电场中的运动，在近几年的各省高考题出现的频率较高，常与动能定理，功能关系等知识点交汇命题.
知识点
如图所示空间分为I、Ⅱ两个足够长的区域，各界面（图中虚线）水平，I区域存在匀强电场E1=1．0×l04 V／m，方向竖直向上；Ⅱ区域存在匀强电场E2=
放，粒子重力忽略不计，求：
12.粒子离开区域I时的速度大小；
13.粒子出区域Ⅱ后加另一个匀强电场，使粒子在此电场作用下经1.0s速度变为零，求此
电场的方向及电场强度E3.
正确答案
4×103 m/s
解析
由动能定理得
得：
考查方向
动能定理
解题思路
根据电场力公式与动能定理即可求得速度值.
易错点
掌握电场力做功的公式，依据动能定理列式解答.
正确答案
50V/m
解析
粒子在Ⅱ区域内受水平向右的库仑力的作用，粒子做类平抛运动，设粒子刚出区域Ⅱ时速度与边界的夹角为
粒子在Ⅱ区域内的运动时间
根绝牛顿第二定律得
由
考查方向
带电粒子在匀强电场中的运动;匀变速直线运动的公式
解题思路
粒子在Ⅱ区域内做类平抛运动，通过牛顿第二定律和速度时间的关系得粒子最终速度，即可根据三角关系得出夹角，再根据速度的大小与夹角，即可求出强度.
易错点
关键根据类平抛规律求出粒子刚出区域Ⅱ时速度大小及方向.
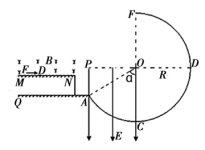
如图所示，水平地面QA与竖直面内的、半径R=4m的光滑圆轨道ACDF相连，FC为竖直直径，DO水平，AO与CO夹角α=600。QA上方有一水平台面MN，MN正上方分布着垂直纸面向里的匀强磁场,磁感强度B=4T。P是竖直线AP与DO的交点，PA的右侧、PO的下面、OC的左侧分布着竖直向下的、场强为E的匀强电场。一个质量m=2kg、电量q=+1C的小滑块（可视为质点）放在MN上，在水平推力F=4N的作用下正以速度V1向右作匀速运动。已知滑块与平台MN的滑动摩擦因数u=0.5；重力加速度g=10m/s2。
15.求小滑块在平台MN上的速度V1
16.小滑块从N点飞出后，恰从A点无碰撞地（沿轨道切线）进入圆轨道AC，为了使小滑块不向内脱离AF间的圆弧轨道，求电场强度E的取值范围
正确答案
解析
解： ①
②
③
由①②③解得：
考查方向
洛伦兹力，平衡条件。
解题思路
对小滑块受力分析，由平衡条件列式可求出。
易错点
解决本题的关键是小滑块以速度V1向右作匀速运动。
正确答案
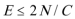
解析
①在A：
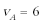
②小滑块不脱离AF的圆弧轨道，刚好滑到D点：VD=0m/s
解出：
③小滑块不脱离AF的圆弧轨道，刚好滑到F点：
解出：
④综上：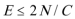
考查方向
磁场中的能量问题
解题思路
由动能定理和牛顿第二定理结合列方程计算。
易错点
小滑块从N到A做平抛运动，由平抛规律求A点的速度vA。
如图所示，在坐标系oxy的第一象限内有Ｅ＝1.0×103Ｖ/m.方向沿y轴负方向的匀强电场，在第四象限有Ｂ＝1Ｔ.方向垂直纸面向里长为10m.宽为1m紧贴x.y轴的匀强磁场。现有质荷比
27.Ａ点到坐标原点Ｏ的距离；
28.粒子从Ａ出发到最终离开磁场的时间。
正确答案
y=2m
解析
带电粒子电场区做类平抛运动，进入磁场时沿-y方向速度为Vy
①
Ａ点到坐标原点Ｏ的距离
y=2m ④
考查方向
带电粒子在复合场中的运动.
解题思路
带电粒子电场区做类平抛运动，根据类平抛运动规律计算竖直方向上的位移的大小即可.
易错点
熟悉类平抛运动的处理方式，把类平抛运动分解成相互垂直方向的匀速直线运动和初速度为0的匀加速直线运动，通过分运动的处理得到合运动的性质．
正确答案
粒子从Ａ出发到最终离开磁场的时间
t=t1+t2=3.57×10-3s
解析
带电粒子第一次在电场中运动时间：
带电粒子在磁场中做匀速圆周运动
所以粒子不会从下边界和右边界射出，且从磁场的上边界第一次射出后再不回磁场了 ⑩
带电粒子在磁场中运动时间：
粒子从Ａ出发到最终离开磁场的时间
t=t1+t2=3.57×10-3s ⑫
考查方向
带电粒子在复合场中的运动.
解题思路
计算粒子的合速度的大小，根据洛伦兹力作为向心力计算在磁场中运动的周期的大小和圆心角，从而计算时间的大小，与在电场中运动的时间的和即为总时间．
易错点
熟悉类平抛运动的处理方式，把类平抛运动分解成相互垂直方向的匀速直线运动和初速度为0的匀加速直线运动，通过分运动的处理得到合运动的性质．画出轨迹，运用几何知识求出磁场中运动的半径，即可求出时间．
如图所示，在水平边界AB和CD间有一匀强电场，电场强度大小E（E未知）.同时存在水平的磁场，EF为左右的分界线。将水平存在的磁场分成向里和向外的匀强磁场，磁感应强度大小相同，均为B（B未知）AB边界上的P点到边界EF的距离为
17.电场强度E的方向
18.O点距离P点的高度h多大；
19.若微粒从O点以v0=
正确答案
E的方向竖直向上（2分）
解析
解:微粒带电量为q、质量为m，轨迹为圆弧，有
qE=mg
解得：
考查方向
带电粒子在匀强磁场中的运动；带电粒子在匀强电场中的运动
解题思路
微粒在进入电磁场前做匀加速直线运动，在电磁场中做匀速圆周运动，电场力与重力应平衡，据此分析和求解场强的方向.
易错点
关键分析出带电粒子在电磁场中运动情况，由受力条件列方程.
正确答案
h=L/2
解析
微粒在磁场中运动速率v1时恰好与AB相切，如图所示：
O1、O2为微粒运动的圆心，O1O2与竖直方向夹角为θ，由几何知识知
微粒半径r1，由几何关系有
由动能定理有
已知
考查方向
带电粒子在匀强磁场中的运动
解题思路
微粒在磁场中运动速率v1时恰好与AB相切，画出运动轨迹，根据几何关系求出轨迹半径；由洛伦兹力公式和牛顿第二定律求出轨迹半径．微粒在进入电磁场前做匀加速直线运动，由动能定理可以求出O到P的距离h.
易错点
关键画出带正电微粒的轨迹图，利用几何关系求解.
正确答案
t=
解析
微粒平抛到AB边界上的M点的时间为t1，水平距离x1，由运动学公式有
代入v0=
微粒在M点时竖直分速度v1=
微粒在磁场中运动周期
由题意有微粒运动时间
微粒运动时间t=
考查方向
平抛运动；带电粒子在匀强磁场中的运动
解题思路
微粒在进入电磁场前做平抛运动，在电磁场中做匀速圆周运动，根据微粒做圆周运动的周期公式求出微粒的运动时间.
易错点
关键要抓住圆周运动的周期性结合平抛运动规律列式求解.
扫码查看完整答案与解析