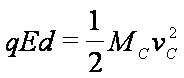- 带电粒子在匀强电场中的运动
- 共205题
边长为l的正方形ABCD区域内存在一个有界匀强电场,电场线平行于纸面,场强为E。质量m、带电量+q的某种粒子从AB边中点O以任意平行纸面方向、大小不变的初速度射入电场,仅在电场力作用下运动。若某个粒子从CD边中点离开,则该粒子射入时初速度方向为 ;若要使所有粒子离开电场时电势能都减小qEl,则入射初速度不能超过 。
正确答案
沿电场线方向
解析
略
知识点
如图所示,A、B为两块平行金属板,A板带正电、B板带负电,两板之间存在着匀强电场,两板间距为d、电势差为U,在B板上开有两个间距为L的小孔。C、D为两块同心半圆形金属板,圆心都在贴近B板的O′处,C带正电、D带负电。两板间的距离很近,两板末端的中心线正对着B板上的小孔,两板间的电场强度可认为大小处处相等,方向都指向O′。半圆形金属板两端与B板的间隙可忽略不计。现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电量为q的带正电微粒(微粒的重力不计)。
求:
(1)微粒穿过B板小孔时的速度多大?
(2)为了使微粒能在CD板间运动而不碰板,CD板间的电场强度大小应满足什么条件?
(3)从释放微粒开始,经过多长时间微粒第1次通过半圆形金属板间的最低点P?
正确答案
见解析。
解析
(1)设微粒穿过B板小孔时的速度为v,根据动能定理,有

得 
(2)微粒进入半圆形金属板后,电场力提供向心力,有

联立①、②,得
(3)微粒从释放开始经t1射出B板的小孔,则

设微粒在半圆形金属板间运动经过t2第一次到达最低点P点,则

所以从释放微粒开始到微粒第一次到达P点经过的时间为
知识点
10.如图所示,粗糙、绝缘的直轨道OB固定在水平桌面上,B端与桌面边缘对齐,A是轨道上一点,过A点并垂直于轨道的竖直面右侧有大小E=1.5×106N/C,方向水平向右的匀强电场。带负电的小物体P电荷量是2.0×10-6C,质量m=0.25kg,与轨道间动摩擦因数μ=0.4,P从O点由静止开始向右运动,经过0.55s到达A点,到达B点时速度是5m/s,到达空间D点时速度与竖直方向的夹角为α,且tanα=1.2。P在整个运动过程中始终受到水平向右的某外力F作用,F大小与P的速率v的关系如表所示。P视为质点,电荷量保持不变,忽略空气阻力,取g=10 m/s2,求:
(1)小物体P从开始运动至速率为2m/s所用的时间;
(2)小物体P从A运动至D的过程,电场力做的功。
正确答案
(1)小物体P在速率从0至2m/s时,所受外力F1=2N,设其做匀变速直线运动的加速度为a1,经过时间△t1速度为v1,则
F1-μmg= ma1 ①
v1=a1△t1 ②
由①②式并代入数据得 △t1= 0.5s ③
说明:①②③式各2分。
(2)小物体P从速率为2m/s运动至A点,受外力F2=6N,设其做匀变速直线运动的加速度为a2则
F2-μmg= ma2 ④
设小物体P从速度v1经过△t2时间,在A点的速度为 v2,则
△t2=0.55s-△t1 ⑤
v2= v1+ a2△t2 ⑥
P从A点至B点,受外力F2=6N、电场力和滑动摩擦力的作用,使其做匀变速直线运动加速度为a3,电荷量为q,在B点的速度为v3,从A点至B点的位移为x1,则
F2-μmg-qE=ma3 ⑦


P 以速度v3滑出轨道右端B点,设水平方向受外力为 F3,电场力大小为FE,有
FE=F3 ⑨
F3与FE 大小相等方向相反,P水平方向所受合力为零,所以,P从点B点开始做初速度为v3的平抛运动。设P从B点运动至D点用时为△t3,水平位移为x2,由题意知

x2= v3△t3 ⑪
设小物体P从A点至D点电场力做功为W,则
W= -qE(x1+x2) ⑫
联立④⑧⑩~⑫式并代入数据得
W=-9.25J ⑬
解析
解析已在路上飞奔,马上就到!
知识点
如图所示,绝缘水平面上相距L=1.6m的空间内存在水平向左的匀强电场E,质量m=0.1kg、带电量q=1×10-7C的滑块(视为质点)以v0=4m/s的初速度沿水平面向右进入电场区域,滑块与水平面间的动摩擦因数μ=0.4(设最大静摩擦力与滑动摩擦力相等)。(g取10m/s2)
(1)如果滑块不会离开电场区域,电场强度E的取值范围多大。
(2)如果滑块能离开电场区域,试在W—F坐标中画出电场力对滑块所做的功W与电场力F的关系图象。
正确答案
见解析
解析
解:(1)小滑块在摩擦力和电场力的作用下,向右做匀减速直线运动,设加速度为a,依题意和牛顿第二定律,有:

又:

若小滑块不会从右侧离开电场区域,由匀变速直线运动规律,有:

联立①②③④并代入数据得:
若小滑块不会从左侧离开电场区域,必须满足:

②⑤⑥可得:
(2)如果小滑块会离开电场区域,电场力F必须满足:
F=qE= q=1×10-7×106≤0.1N ⑧
或 F=qE = 1×10-7×4×106>0.4N ⑨
若F≤0.1N,小滑块将从右侧离开电场区域,此过程小滑块在电场中的位移s=1.6m,则电场力做功
若F>0.4N,小滑块将从左侧离开电场区域,此过程小滑块在电场中的位移s=0,电场力做功为0,即W=0
知识点
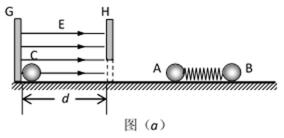
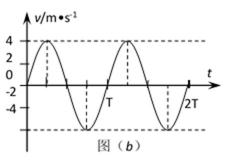
如图,光滑水平面上固定着一对竖直放置的平行金属板G和H。在金属板G右壁固定一个可视为质点的小球C,其质量为 MC=0.01kg、带电量为q=+1×10-5C。G、H两板间距离为d=10cm,板H下方开有能让小球C自由通过的小洞。质量分别为MA=0.01kg和MB=0.02kg的不带电绝缘小球A、B用一轻质弹簧连接,并用细线栓连使弹簧处于压缩状态,静放在H板右侧的光滑水平面上,如图(a)所示。现将细线烧断,小球A、B在弹簧作用下做来回往复运动(A球不会进入G、H两板间)。以向右为速度的正方向,从烧断细线断开后的某时刻开始计时,得到A球的速度—时间图象如图(b)所示。
(1)求在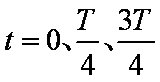
(2)若G、H板间是电场强度为E=8×104V/m的匀强电场,在某时刻将小球C释放,则小球C离开电场时的速度为多大?若小球C以离开电场时的速度向右匀速运动,它将遇到小球A,并与之结合在一起运动,试求弹簧的最大弹性势能的范围。
正确答案
见解析。
解析
(1)对于小球A、B与轻质弹簧组成的系统,当烧断细线后动量守恒,有
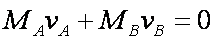
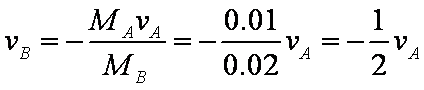
当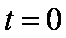
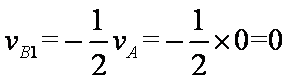
当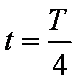
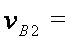
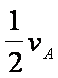
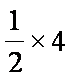
当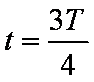
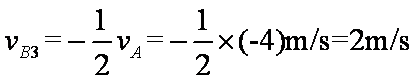
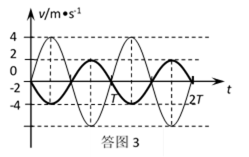
小球B的速度—时间图象如答图3所示。
(2)当金属板间加有匀强电场时,电场力对小球做功,小球获得初动能并离开金属板。
由动能定理,有
得 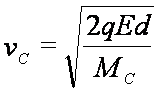
因水平方向A、B、C三小球系统不受外力,故系统动量守恒。
由此可得,不论A、C两球何时何处相碰,三球的共同速度是一个定值,即三球速度相同时的总动能是一定值。
由MCvC=(MA+MB+MC)v共 , 解得v共 =1m/s
当三球速度相同时弹簧的弹性势能最大。
当A球在运动过程中速度为4m/s且与C球同向时,跟C球相碰,系统损失能量最小(为0),此情况下三球在运动过程中弹簧具有的最大弹性势能设为E1
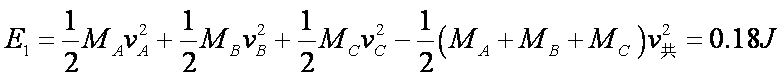
当A球在运动过程中速度为4m/s与C球反向时,跟C球相碰,系统损失能量最大,此情况下三球运动的过程中弹簧具有的最大弹性势能设为E2
由MCvC–MAvA=(MA + MC)v3 , 解得v3 =0
E2=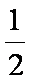
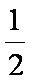
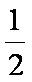
由上可得:弹簧具有的最大弹性势能的可能值在0.02J ~ 0.18J的范围内。
知识点
扫码查看完整答案与解析