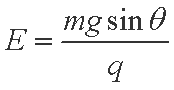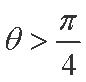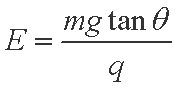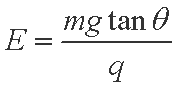- 电磁学
- 共4057题
如图12所示，用长为L的绝缘细线悬挂一带电小球，小球的质量为m、电荷量为q。现加一水平向左的匀强电场，平衡时小球静止于M点，细线与竖直方向成θ角。
（1）求匀强电场的电场强度E的大小；
（2）在某一时刻细线断裂，同时质量也为m的不带电的一小块橡皮泥，以水平向左的速度v0击中小球并与小球结合成一体，求击中后瞬间复合体的速度大小；
（3）若原小球离地高为h，求复合体落地过程中的水平位移大小。
正确答案
见解析。
解析
（1）小球受力平衡时有 
（2）橡皮泥撞击小球的过程中，水平方向动量守恒，
mv0＝（m+ m）v
所以
（3）复合体水平方向的加速度为
复合体落地时间为
复合体在水平方向做匀加速直线运动，水平位移为x
知识点
两电荷量分别为q1和q2的点电荷放在x轴上的 O、M两点，两电荷连线上各点电势φ随x变化的关系如图所示，其中A、N两点的电势均为零，ND段中的C点电势最高，则( )
正确答案
解析
略
知识点
在空间某一匀强电场中，将一质量为m，电荷量为q的小球由静止释放，带电小球的运动轨迹为一直线，该直线与竖直方向成锐角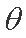
A由于小球所受的电场力和重力做功均与路径无关，故小球的机械能守恒
B若
C若
D若
正确答案
解析
略
知识点
如图甲所示，两个点电荷Q1、Q2固定在x轴上距离为L的两点，其中Q1带正电位于原点O，a、b是它们连线延长线上的两点，其中b点与O点相距3L。现有一带正电的粒子q以一定的初速度沿x轴从a点开始经b点向远处运动（粒子只受电场力作用），设粒子经过a，b两点时的速度分别为va，vb，其速度随坐标x变化的图象如图乙所示，则以下判断正确的是
正确答案
解析
略
知识点
如图所示，水平固定的矩形金属板A带电量为Q，电势为零，从金属板中心O处释放一质量为m、带电量为+q的小球，由于电场力的作用，小球竖直上升的最大高度可达金属板中心竖直线上的C点，已知OC＝h，重力加速度为g，又知道小球过竖直线上B点时的速度最大，由此可确定Q所形成的电场中的物理量是
正确答案
解析
略。
知识点
一带负电荷的质点，在电场力作用下沿曲线abc从a减速运动到c。则关于b点电场强度E的方向，可能正确的是（虚线是曲线在b点的切线）（ ）
A
B
C
D
正确答案
解析
略
知识点
如图所示，在真空中固定两个等量异号点电荷+Q和-Q，图中O点为两点电荷的连线中点，P点为连线上靠近
AM、N两点的电势相同
BM、N两点的电场强度相同
C将带正电的试探电荷从M点沿直线移到N点的过程中，电荷的电势能先增大后减小
D只将
正确答案
解析
略。
知识点
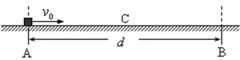
如图所示，质量为m带电量为+q的小滑块以大小为v0的初速度从A点进入宽度为d的AB绝缘水平面。当滑块运动至中点C时，速度大小为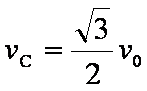
正确答案
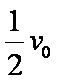
解析
略
知识点
如图所示，两个等量异种点电荷+Q、-Q分别固定在处于真空中的正方体的两个顶点上，下列判断正确的是
正确答案
解析
略。
知识点
一半径为R的光滑圆环竖直放在水平向右场强为E的匀强电场中，如图所示，环上a、c是竖直直径的两端，b、d是水平直径的两端，质量为m的带电小球套在圆环上，并可沿环无摩擦滑动。现使小球由a点静止释放，沿abc运动到d点时速度恰好为零，由此可知，小球在b点时（ ）
正确答案
解析
略
知识点
如图1所示，一长为l且不可伸长的绝缘细线，一端固定于O点，另一端拴一质量为m的带电小球。空间存在一场强为E、方向水平向右的匀强电场。当小球静止时，细线与竖直方向的夹角为θ=37°。已知重力加速度为g，sin37°=0.6，cos37°=0.8。
（1）判断小球所带电荷的性质，并求出小球所带的电荷量q；
（2）如图2所示，将小球拉至A点，使细线处于水平拉直状态。释放小球，小球由静止开始向下摆动，当小球摆到B点时速度恰好为零。
a．求小球摆动过程中最大速度vm的大小；
b．三位同学对小球摆动到B点时所受合力的大小F合进行了讨论：第一位同学认为
正确答案
见解析。
解析
（1）小球带正电。
因为
所以
（2）a．小球在场中静止时的位置是小球摆动过程中的平衡位置，故小球到达此位置时速度最大。根据动能定理有
所以
b．第三位同学的观点正确。
【方法一】根据对称性，小球摆到B点时所受的合力与小球在A点时所受合力的大小相等。小球到达A点时的受力如图所示，因为TA=qE，所以小球所受合力的大小F合=mg。
【方法二】设小球摆到B点时，细线与竖直方向的夹角为α，根据动能定理有
又因为
所以 
则
知识点
如图，光滑水平面上存在水平向右、场强为
（1） 物体
（2） 物体
（3） 弹簧的最大弹性势能。
正确答案
见解析。
解析
（1）小球受到合外力为
（2）小球离开电场时的速度为
碰撞过程中损失的机械能为
则：
解得： 
（3）由能量守恒得：
知识点
14.下列说法正确的是（ ）
A电荷的周围既有电场也有磁场，反映了电和磁是密不可分的
B由电场强度的定义式
C法拉第首先总结出磁场对电流作用力的规律
D“电生磁”和“磁生电”都是在变化、运动的过程中才能出现的效应
正确答案
解析
静止的电荷周围只有电场，没有磁场，A错；E的正负与检验电荷无关，B错；安培首先总结出磁场对电流的作用，C错。
知识点
一粒子从A点射入电场，从B点射出，电场的等势面和粒子的运动轨迹如图所示，图中左侧前三个等势面平行，不计粒子的重力。则正确的是
正确答案
解析
略
知识点
如图所示，一质量m=0.1kg、电量q=1.0×10-5 C的带正电小球（可视作点电荷），它在一高度和水平位置都可以调节的平台上滑行一段距离后平抛，并沿圆弧轨道下滑。A、B为圆弧两端点，其连线水平，已知圆弧半径R=1.0m，平台距AB连线的高度h可以在0.2m-0.8m.之间调节。有一平行半径OA方向的匀强电场E，只存在圆弧区域内。为保证小球从不同高度h平抛，都恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道，小球平抛初速度v0和h满足如图所示的抛物线，同时调节平台离开A点的距离合适。不计空气阻力，取g=10m/s2，求：
（1）小球在空中飞行的最短时间t；
（2）平台离开A的水平距离x范围；
（3）当h=0.2m且E=2.5×104N/C时，小球滑到最低点C点的速度v；
（4）为了保证小球在圆轨道内滑动到C点的速度都是（3）中的v，则电场力F=qE的大小应与平台高度h满足的关系。（通过列式运算说明）
正确答案
（1）当平台高度为0.2m时，空中飞行的最短时间t=
（2）因为小球从不同高度h平抛，都恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道，所以小球进入圆弧轨道时时的速度方向不变，设此速度与竖直方向成α角。
tgα=
v02=2ghtan2α
由图像中当h=0.8m时，v0=3m/s代入上式得
9=2×10×0.8×tg2α
tgα=0.75 α=370 则θ=1060
所以v02=11.25h
当h=0.2m时, v0=1.5m/s
平台离开A的最小距离为s1= v0t=1.5×0.2=0.3m
同理得平台离开A的最大距离为s2= v0
（3）小球到达A点时的速度vA=
从A点到C点，由动能定理得
mgR(1-cos530)-qE R(1-cos530)= 
代入数据，解得vC=3.5m/s
（4）从A点到C点，由动能定理得
mgR(1-cos530)-FR(1-cos530)=
=
=
代入数据得32F=125h-17
或
解析
略
知识点
扫码查看完整答案与解析