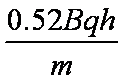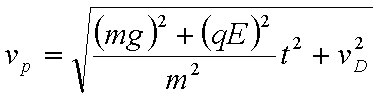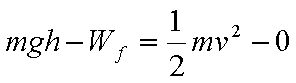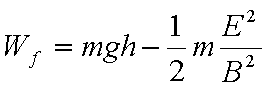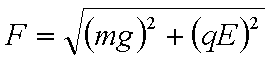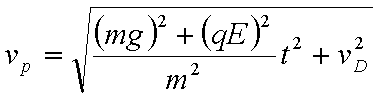- 电磁学
- 共4057题
扭摆器是同步辐射装置中的插入件,能使粒子的运动轨迹发生扭摆。其简化模型如图:Ⅰ、Ⅱ两处的条形匀强磁场区边界竖直,相距为L,磁场方向相反且垂直纸面。一质量为m、电量为-q、重力不计的粒子,从靠近平行板电容器MN板处由静止释放,极板间电压为U,粒子经电场加速后平行于纸面射入Ⅰ区,射入时速度与水平和方向夹角θ=30º。
(1)当Ⅰ区宽度L1=L、磁感应强度大小B1=B0时,粒子从Ⅰ区右边界射出时速度与水平方向夹角也为30º,求B0及粒子在Ⅰ区运动的时间t。
(2)若Ⅱ区宽度L2=L1=L、磁感应强度大小B2=B1=B0,求粒子在Ⅰ区的最高点与Ⅱ区的最低点之间的高度差h。
(3)若L2=L1=L、B1=B0,为使粒子能返回Ⅰ区,求B2应满足的条件。
(4)若B1≠B2,L1≠L2,且已保证了粒子能从Ⅱ区右边界射出。为使粒子从Ⅱ区右边界射出的方向与从Ⅰ区左边界射出的方向总相同,求B1、B2、L1、L2之间应满足的关系式。
正确答案
见解析。
解析
(1)如图1所示,设粒子射入磁场I区的速度为v,在磁场I区做圆周运动半径为


由几何关系得
联立①②③得
设粒子在I区做圆周运动周期为T,运动时间为t,


联立①③⑤⑥式解得
(2)设粒子在磁场II区做圆周运动半径为

由几何知识得 
联立②③⑧⑨式解得
(3)如图2所示,为使粒子能再次返回到I区应满足

联立①⑧11式解得
(4)如图3(或图4)所示,设粒子射出磁场I区时速度与水平方向的夹角为α,由几何知识可得

联立②⑧1314式解得
知识点
一圆筒的横截面如图所示,其圆心为O。筒内有垂直于纸面向里的匀强磁场,磁感应强度为B。圆筒下面有相距为d的平行金属板M、N,其中M板带正电荷,N板带等量负电荷。质量为m、电荷量为q的带正电粒子自M板边缘的P处由静止释放,经N板的小孔S以速度v沿半径SO方向射入磁场中,粒子与圈筒发生两次碰撞后仍从S孔射出,设粒子与圆筒碰撞过程中没有动能损失,且电荷量保持不变,在不计重力的情况下,求:
(1)M、N间电场强度E的大小;
(2)圆筒的半径R:
(3)保持M、N间电场强度E不变,仅将M板向上平移2/3d,粒子仍从M板边缘的P处由静止释放粒子自进入圆筒至从S孔射出期间,与圆筒的碰撞次数n。
正确答案
见解析
解析
解析:
知识点
如图所示,正方形绝缘光滑水平台面WXYZ边长l=1.8m,距地面h=0.8m。平行板电容器的极板CD间距d=0.1m且垂直放置于台面。C板位于边界WX上,D板与边界WZ相交处有一小孔。电容器外的台面区域内有磁感应强度B=1T,方向竖直向上的匀强磁场。电荷量q=5×10-13C的微粒静止于W处,在CD间加上恒定电压U=2.5V,板间微粒经电场加速后由D板所开小孔进入磁场(微粒始终不与极板接触),然后由XY边界离开台面。在微粒离开台面瞬时,静止于X正下方水平地面上A点的滑块获得一水平速度,在微粒落地时恰好与之相遇。假定微粒在真空中运动、极板间电场视为匀强电场,滑块视为质点。滑块与地面间的动摩擦因数μ=0.2,取g=10m/s2。
(1)求微粒在极板间所受电场力的大小并说明两板的极性;
(2)求由XY边界离开台面的微粒的质量范围;
(3)若微粒质量m0=1×10-13kg,求滑块开始运动所获得的速度。
正确答案
见解析。
解析
(1)微粒在极板间所受电场力大小为F=
由微粒在磁场中的运动可判断微粒带正电荷,微粒由极板间电场加速,故C板为正极,D板为负极。
(2)若微粒的质量为m,刚进入磁场时的速度大小为v,由动能定理:Uq=
微粒在磁场中做匀速圆周运动,洛仑兹力充当向心力,若圆周运动半径为R,有:
微粒要从XY边界离开台面,则圆周运动的边缘轨迹如图所示,半径的极小值与极大值分别为
(3)如图,微粒在台面以速度v做以O点为圆心,R为半径的圆周运动,从台面边缘P点沿与XY边界成θ角飞出做平抛运动,落地点Q,水平位移s,下落时间t。设滑块质量为M,滑块获得速度v0后在t内沿与平台前侧面成ф角方向,以就爱上的a做匀减速直线运动到Q,经过位移为k。由几何关系,可得
cosθ=

对于滑块,由牛顿定律及运动学方程,有
μMg=Ma,
再由余弦定理:k2=s2+(d+Rsinθ)2-2s(d+Rsinθ)cosθ
及正弦定理:
联立并代入数据解得:v0=4.15m/s,ф=arcsin0.8(或ф=53°)
知识点
如图,某一新型发电装置的发电管是横截面为矩形的水平管道,管道的长为L、宽度为d、高为h,上下两面是绝缘板,前后两侧面M、N是电阻可忽略的导体板,两导体板与开关S和定值电阻R相连。整个管道置于磁感应强度大小为B,方向沿z轴正方向的匀强磁场中。管道内始终充满电阻率为ρ的导电液体(有大量的正、负离子),且开关闭合前后,液体在管道进、出口两端压强差的作用下,均以恒定速率v0沿x轴正向流动,液体所受的摩擦阻力不变。
(1)求开关闭合前,M、N两板间的电势差大小U0;
(2)求开关闭合前后,管道两端压强差的变化Δp;
(3)调整矩形管道的宽和高,但保持其它量和矩形管道的横截面S=dh不变,求电阻R可获得的最大功率Pm及相应的宽高比d/h的值。
正确答案
(1)设带电离子所带的电量位q,当其所受的洛伦兹力与电场力平衡时,U0保持恒定,有

得:
(2)设开关闭合前后,管道两端压强差分别为p1、p2,液体所受的摩擦阻力均为f,开关闭合后管道内液体受到的安培力为F安,有:p1hd=f,③
p2hd=f+F安,④
F安=Bid⑤
根据欧姆定律,有
两道题板间液体的电阻
由②③④⑤⑥⑦式得:
(3)电阻R获得的功率为:

当
电阻R获得的最大功率
解析
略。
知识点
在如图所示的竖直平面内。水平轨道CD和倾斜轨道GH与半径r =
(1)小物体P1在水平轨道CD上运动速度v的大小;
(2)倾斜轨道GH的长度s。
正确答案
见解析
解析
(1)设小物体P1在匀强磁场中运动的速度为v,受到向上的洛伦兹力为F1,受到的摩擦力为f,则
F1=qvB ①
f=μ(mg-F1) ②
由题意,水平方向合理为零
F-f=0 ③
联立①②③式,代入数据解得
v=4 m/s ④
说明:①③式各1分,②④式各2分
(2)设P1在G点的速度大小为vG,由于洛伦兹力不做功,根据动能定理

P1在GH上运动,受到重力、电场力和摩擦力的作用,设加速度为a1,根据牛顿第二定律
qEcosθ-mgsinθ-μ(mgcosθ+qEsinθ)=ma1 ⑥
P1与P2在GH上相遇时,设P1在GH运动的距离为s1,则

设P2质量为m2,在GH上运动的加速度为a2,则
m2gsinθ-μm2gcosθ+qEsinθ)=m2a2 ⑧
P1与P2在GH上相遇时,设P2在GH运动的距离为s2,则

联立⑤~⑨式,代入数据得
s=s1+s2 ⑩
s=0.56 m ⑾
知识点
如图所示的平面直角坐标系xoy,在第Ⅰ象限内有平行于














(1)电场强度E的大小;
(2)粒子到达
(3)

正确答案
见解析
解析
(1)设粒子在电场中运动的时间为t,则有
联立以上各式可得
(2)粒子到达a点是沿负y方向的分速度为

(3)粒子在磁场中运动是,有
当粒子从b点射出是,磁场的磁感应强度为最小值,此时有
知识点
同步加速器在粒子物理研究中有重要的应用,其基本原理简化为如图所示的模型。M、N为两块中心开有小孔的平行金属板。质量为m、电荷量为+q的粒子A(不计重力)从M板小孔飘入板间,初速度可视为零。每当A进入板间,两板的电势差变为U,粒子到达加速,当A离开N板时,两板的电荷量均立即变为零。两板外部存在垂直纸面向里的匀强磁场,A在磁场作用下做半径为R的圆周运动,R远大于板间距离。A经电场多次加速,动能不断增大,为使R保持不变,磁场必须相应地变化。不计粒子加速时间及其做圆周运动产生的电磁辐射,不考虑磁场变化对粒子速度的影响及相对论效应。求:
(1)A运动第1周时磁场的磁感应强度B1的大小。
(2)在A运动第n周的时间内电场力做功的平均功率
(3)若有一个质量也为m、电荷量为+kq(k为大于1的整数)的粒子B(不计重力)与A同时从M板小孔飘入板间,A、B初速度均为零,不计两者间的相互作用,除此之外,其他条件均不变。下图中虚线、实线分别表示A、B的运动轨迹。在B的轨迹半径远大于板间距离的前提下,请指出哪个图能定性地反映A、B的运动轨迹,并经推导说明理由。
正确答案
(1)
(2)
(3)图A,
解析
(1)设A经电场第一次加速后速度为

A在磁场中做匀速圆周运动,所受洛伦兹力充当向心力

由①②得

(2)设A经


设A做第


设A运动第


在该段时间内电场力做功的平均功率为

由④⑤⑥⑦解得

(3)A图能定性地反映A,B运动的轨迹。
A经过


由上可知,



经


由题设条件并考虑到⑤式,对A有
设B的轨迹半径为
比较上述两式得
上式表明,运动过程中B的轨迹半径始终不变。
由以上分析可知,两粒子运动的轨迹如图A所示。
知识点
如图所示,MN、PQ是平行金属板,板长为L,两板间距离为d,PQ板带正电,MN板带负电,在PQ板的上方有垂直纸面向里的匀强磁场,一个电荷量为q、质量为m的带负电粒子以速度v0从MN板边缘沿平行于板的方向射入两板间,结果粒子恰好从PQ板左边缘飞进磁场,然后又恰好从PQ板的右边缘飞进电场,不计粒子重力,试求:
(1)两金属板间所加电压U的大小;
(2)匀强磁场的磁感应强度B的大小。
正确答案
(1)
解析
(1)分析知,粒子的运动轨迹如图所示,
粒子在电场中运动的时间为t=
加速度为a=
偏转位移为
y=

由题意知y=d
得U=
(2)由
得粒子离开电场时的竖直分速度为vy=
速度大小为v=

设速度方向和PQ所在直线的夹角为θ,
sinθ=

粒子在磁场中的运动半径为
R=

由qBv=m
得R=
B=
知识点
如题9图所示,在无限长的竖直边界NS和MT间充满匀强电场,同时该区域上、下部分分别充满方向垂直于NSTM平面向外和向内的匀强磁场,磁感应强度大小分别为B和2B,KL为上下磁场的水平分界线,在NS和MT边界上,距KL高h处分别有P、Q两点,NS和MT间距为1.8h。质量为m、带电量为+q的粒子从P点垂直于NS边界射入该区域,在两边界之间做圆周运动,重力加速度为g。
(1)求该电场强度的大小和方向。
(2)要使粒子不从NS边界飞出,求粒子
(3)若粒子能经过Q点从MT边界飞出,求粒子入射速度的所有可能值。
正确答案
答案:(1)E=mg/q,方向向上;(2)

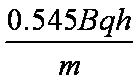
解析
知识点
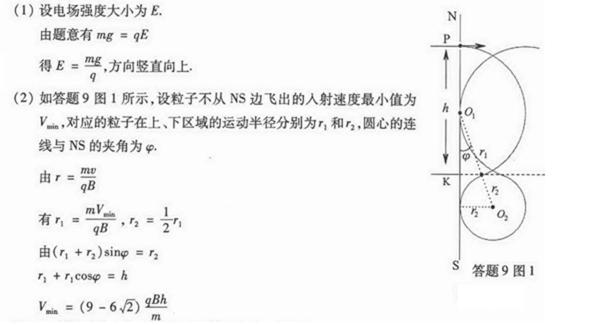
22. 如图,绝缘粗糙的竖直平面MN左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为E,磁场方向垂直纸面向外,磁感应强度大小为B。一质量为m、电荷量为q的带正电的小
(1)求小滑块运动到C点时的速度大小vc;
(2)求小滑块从A点运动到C点过程中克服摩擦力做的功Wf;
(3)若D点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置,当小滑块运动到D点时撤去磁场,此后小滑块继续运动到水平地面上的P点。已知小滑块在D点时的速度大小为vD,从D点运动到P点的时间为t,求小滑块运动到P点时速度的大小vp。
正确答案
(1)E/B (2
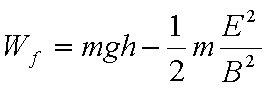
(1)由题意知,根据左手定则可判断,滑块在下滑的过程中受水平向左的洛伦兹力,当洛伦兹力等于电场力qE时滑块离开MN开始做曲线运动,即Bqv=qE
解得:v=E/B
(2)从A到C根据动能定理:
解得:
(3)设重力与电场力的合力为F,由图意知,在D点速度vD的方向与F地方向垂直,从D到P做类平抛运动,在F方向做匀加速运动a=F/m,t时间内在F方向的位移为
从D到P,根据动能定理: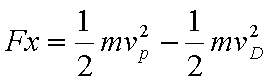
联立解得:
解析
解析已在路上飞奔,马上就到!
知识点
如图所示,在两个水平放置的平行金属板之间,电场和磁场的方向相互垂直。一束带电粒子(不计重力)沿着直线穿过两板间的空间而不发生偏转。则这些粒子一定具有相同的
正确答案
解析
略
知识点
如图所示,AB、CD是处在方向垂直纸面向里、磁感应强度为的匀强磁场的两条金属导轨(足够长),导轨宽度为d,导轨通过导线分别与平行金属板MN相连,有一与导轨垂直且始终接触良好的金属棒ab以某一速度
(1)金属棒ab做匀速直线运动速度的大小B?
(2) 粒子到达H点时的速度多大?
(3)要使粒子不能回到y轴边界,电场强度以满足什么条件?
正确答案
见解析。
解析
金属棒ab在切割磁感线过程中产生的感应电动势为:

设粒子在F进入磁场时的速度为

由几何知识可得(如图)

粒子在通过MN过程中由动能定理得:

联解以上各式得:

(2)从D到C只有电场力对粒子做功,电场力做功与路径无关,根据动能定理,有

解得:

(3)
要使粒子不能回到y轴边界,
即 
知识点
24.如图所示,直径分别为D和2D的同心圆处于同一竖直面内,O为圆心,GH为大圆的水平直径。两圆之间的环形区域(Ⅰ区)和小圆内部(Ⅱ区)均存在垂直圆面向里的匀强磁场。间距为d的两平行金属极板间有一匀强电场,上极板开有一小孔。一质量为m、电量为+q的粒子由小孔下方
(1)求极板间电场强度的大小;
(2)若粒子运动轨迹与小圆相切,求Ⅰ区磁感应强度的大小;
(3)若Ⅰ区、Ⅱ区磁感应强度的大小分别为

正确答案
(1)
(2)

(3)7πD;
解析:
由图可知,粒子每次从磁场Ⅱ区域进入Ⅰ区域速度方向偏离300,可知粒子往复转过12此后可再次经过H点;粒子一次循环走过的路程为
代入解得:
解析
解析已在路上飞奔,马上就到!
知识点
飞行时间质谱仪可以根据带电粒子的飞行时间对气体分子进行分析。如图所示,在真空状态下,自脉冲阀P喷出微量气体,经激光照射产生不同正离子,自a板小孔进入a、b间的加速电场,从b板小孔射出,沿中线方向进入M、N板间的方形区域,然后到达紧靠在其右侧的探测器。已知极板a、b间的电压为U0,间距为d,极板M、N的长度和间距均为L。不计离子重力及经过a板时的初速度。
(1)若M、N板间无电场和磁场,请推导出离子从a板到探测器的飞行时间t
与比荷k(k=
(2)若在M、N间只加上偏转电压U1,请论证说明不同正离子的轨迹是否重合;
(3)若在M、N间只加上垂直于纸面的匀强磁场。已知进入a、b间的正离子有一价和二价的两种,质量均为m,元电荷为e。要使所有正离子均能通过方形区域从右侧飞出,求所加磁场的磁感应强度的最大值Bm。
正确答案
见解析。
解析
(1)带电离子在平行板a、b间运动时,根据动能定理 
解得:
带电离子在平行板a、b间的加速度
所以,带电离子在平行板a、b间的运动时间
带电离子在平行板M、N间的运动时间
所以,带电离子的全部飞行时间
(2)正离子在平行板M、N间水平方向运动位移为x时,在竖直方向运动的位移为y。
水平方向满足 
竖直方向满足 
加速度 
由上述②、③、④式得:
⑤式是正离子的轨迹方程,与正离子的质量和电荷量均无关。所以,不同正离子的轨迹是重合的。
(3)当M、N间磁感应强度大小为B时,离子做圆周运动,满足

由上述①、⑥两式,解得:带电离子的轨道半径
上式表明:在离子质量一定的情况下,离子的电荷量越大,在磁场中做圆周运动的半径越小,也就越不容易穿过方形区从右侧飞出。所以,要使所有的一价和二价正离子均能通过方形区从右侧飞出,只要二价正离子能从方形区飞出即可。当二价正离子刚好能从方形区域飞出时的磁感应强度为满足题目条件的磁感应强度的最大值。
设当离子刚好通过方形区从右侧飞出时的轨道半径为R,由几何关系得
解得: 
将二价正离子的电量2e代入⑦式得:
由⑧、⑨式得:
知识点
如图所示,坐标系xOy在竖直平面内,x轴正方向水平向右,y轴正方向竖直向上。y<0的区域有垂直于坐标平面向外的匀强磁场,磁感应强度大小为B;在第一象限的空间内有与x轴平行的匀强电场(图中未画出);第四象限有与x轴同方向的匀强电场;第三象限也存在着匀强电场(图中未画出)。一个质量为m、电荷量为q的带电微粒从第一象限的P点由静止释放,恰好能在坐标平面内沿与x轴成θ=30°角的直线斜向下运动,经过x轴上的a点进入y<0的区域后开始做匀速直线运动,经过y轴上的b点进入x<0的区域后做匀速圆周运动,最后通过x轴上的c点,且Oa=Oc。已知重力加速度为g,空气阻力可忽略不计,求:
(1)第一象限电场的电场强度E1的大小及方向;
(2)带电微粒由P点运动到c点的过程中,其电势能的变化量大小;
(3)带电微粒从a点运动到c点所经历的时间。
正确答案
见解析。
解析
(1)在第一象限内,带电微粒从静止开始沿Pa做匀加速直线运动,受重力mg和电场力qE1的合力一定沿Pa方向,电场力qE1一定水平向左。
带电微粒在第四象限内受重力mg、电场力qE2和洛仑兹力qvB做匀速直线运动,所受合力为零。分析受力可知微粒所受电场力一定水平向右,故微粒一定带正电。
所以,在第一象限内E1方向水平向左(或沿x轴负方向)。
根据平行四边形定则,有 mg=qE1tanθ
解得 E1=
(2)带电粒子从a点运动到c点的过程中,速度大小不变,即动能不变,且重力做功为零,所以从a点运动到c点的过程中,电场力对带电粒子做功为零。
由于带电微粒在第四象限内所受合力为零,因此有 qvBcosθ=mg
带电粒子通过a点的水平分速度vx=vcosθ=
带电粒子在第一象限时的水平加速度ax=qE1/m=
带电粒子在第一象限运动过程中沿水平方向的位移x=
由P点到a点过程中电场力对带电粒子所做的功W电=qE1x=
因此带电微粒由P点运动到c点的过程中,电势能的变化量大小
ΔE电=
(3)在第三象限内,带电微粒由b点到c点受重力mg、电场力qE3和洛仑兹力qvB做匀速圆周运动,一定是重力与电场力平衡,所以有
qE3=mg
设带电微粒做匀速圆周运动的半径为R,根据牛顿第二定律,有 qvB=mv2/R
带电微粒做匀速圆周运动的周期
T=
带电微粒在第三象限运动的轨迹如图所示,连接bc弦,因Oa=Oc,所以Δabc为等腰三角形,即∠Ocb=∠Oab=30°。过b点做ab的垂线,与x轴交于d点,因∠Oba=60°,所以∠Obd=30°, 因此Δbcd为等腰三角形,bc弦的垂直平分线必交于x轴上的d点,即d点为轨迹圆的圆心。
所以带电粒子在第四象限运动的位移xab=Rcotθ=
其在第四象限运动的时间t1=
由上述几何关系可知,带电微粒在第三象限做匀速圆周运动转过的圆心角为120°,即转过1/3圆周,所以从b到c的运动时间 t2=
因此从a点运动到c点的时间 t=t1+t2=

知识点
扫码查看完整答案与解析