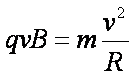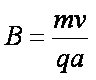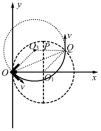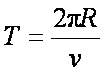- 电磁学
- 共4057题
如图所示,在直角坐标系xoy平面的第Ⅱ象限内有半径为r的圆o1分别与x轴、y轴相切于C(-r,0)、D(0,r) 两点,圆o1内存在垂直于xoy平面向外的匀强磁场,磁感应强度为B,与y轴负方向平行的匀强电场左边界与y轴重合,右边界交x轴于G点,一带正电的A粒子(重力不计)电荷量为q、质量为m,以某一速率垂直于x轴从C点射入磁场,经磁场偏转恰好从D点进入电场,最后从G点以与x轴正向夹角为45°的方向射出电场,求:
(1)A粒子在磁场区域的偏转半径及OG之间的距离;
(2)该匀强电场的电场强度E;
(3)若另有一个与A的质量和电荷量均相同、速率也相同的粒子A′,从C点沿与x轴负方向成30°角的方向射入磁 场,则粒子A′再次回到x轴上某点时,该点的坐标值为多少?
正确答案
见解析。
解析
(1)设粒子A射入磁场时的速率为v0 ,其在磁场中做圆周运动的圆心必在x轴上,设其圆心为OA,连接OAC、OAD,则OAC=OAD=r,所以OA与O点重合,故A粒子在磁场区域的偏转半径也是r. (2分)
A粒子运动至D点时速度与y轴垂直,粒子A从D至G作类平抛运动,设其加速度为a,在电场中运行的时间为t,由平抛运动的规律可得:
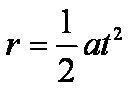
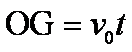
由运动学知识可得:
联立①②③解得: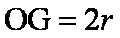
(2)粒子A的轨迹圆半径为r ,由洛仑兹力和向心力公式可得:

由牛顿运动定律和电场力公式可得:
联立①②⑤⑥解得: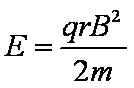
(3)设粒子A′在磁场中圆周运动的圆心为O′ ,因为∠O′ CA′ =90°,O′C=r,以 O′为圆心、r为半径做A′的轨迹圆交圆形磁场O1于H点,则四边形CO′H O1为菱形,故O′H∥y轴,粒子A′ 从磁场中出来交y轴于I点,HI⊥O′H,所以粒子A′也是垂直于y轴进入电场。(2分)
设粒子A′从J点射出电场,交x轴于K点,因与粒子A在电场中的运动类似,由(1)式可得:
OI-JG=r ⑧(2分)
又OI=r+rcos30° ⑨ (1分)
由⑧⑨式解得:JG=rcos30°=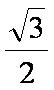
根据图中几何知识可得:∠JKG=45°,GK=GJ ⑩
所以粒子A′再次回到x轴上的坐标为(
知识点
如图所示,R1=R2=40Ω,R,3=25Ω,电源的内电阻r=5Ω,AB是一个电容器,电容器板间距是d=8cm,板长为L=8cm,电容器间有一垂直纸面方向的匀强磁场,磁感应强度B=0.5T。当开关闭合时,电容间有一电量q=8×10-4C,质量为m=8.0×-8kg的带正电的粒子能向右以500m/s匀速穿过这个区域,忽略重力影响。
⑴判断磁场的具体方向;
⑵求电源电动势;
⑶若断开开关S,带电粒子从左边中间射入,试判断该粒子能否射出该区域?若能射出该区域,求它射出该区域时,带电粒子的侧向位移及偏角。
正确答案
见解析。
解析
⑴若粒子带正电,则它所受的电场力向下,而洛伦兹力必然向上,由左手定则可以判断该区域的磁场方向垂直纸面向里。(2分)
⑵带电粒子在电场中所受的电场力为F=qE (1分) ①,板间的电场强度:
洛伦兹力f=qvB (1分)②,两力平衡,则有F=f (1分) ③
联立解得:U=dvB=8×10-2×500×0.5V=20V (1分)④
电路中的电流为:
而R1、R1并联的总电阻为R12=20Ω,则电源电动势为:
ε=I(R12+r)+U=0.8×(20+5)+20=40(V) (2分)
⑶当断开开关时,AB间的电场消失,带电粒子在洛伦兹力作用下
发生偏转的情况如图所示
洛伦兹力提供向心力:
则半径为:
则:侧向位移为:
偏角的正弦值为:
知识点
如图所示,在坐标系xoy的第一、第三象限内存在相同的匀强磁场,磁场方向垂直于xoy面向里;第四象限内有沿y轴正方向的匀强电场,电场强度大小为E,一质量为

(1)求粒子过Q点时速度的大小和方向。
(2)若磁感应强度的大小为一定值B0,粒子将以垂直y轴的方向进入第二象限,求B0;
(3)若磁感应强度的大小为另一确定值,经过一段时间后粒子将再次经过Q点,且速度与第一次过Q点时相同,求该粒子相邻两次经过Q点所用的时间。
正确答案
(1)
(2)
(3)
解析
(1)设粒子在电场中运动的时间为




由运动学公式得




联立得

(2)设粒子做圆周运动的半径为


由牛顿第二定律得

联立得
(3)设粒子做圆周运动的半径为







粒子在第二、第四象限的轨迹为长度相等的线段,得

设粒子相邻两次经过Q点所用的时间为t,则有

联立以上得

知识点
电子扩束装置由电子加速器、偏转电场和偏转磁场组成。偏转电场的极板由相距为d的两块水平平行放置的导体板组成,如图甲所示。大量电子由静止开始,经加速电场加速后,连续不断地沿平行板的方向从两板正中间OO'射入偏转电场。当两板不带电时,这些电子通过两板之间的时间为2t0;当在两板间加最大值为U0、周期为2t0的电压(如图乙所示)时,所有电子均能从两板间通过,然后进入竖直宽度足够大的匀强磁场中,最后打在竖直放置的荧光屏上。已知磁场的磁感应强度为B,电子的质量为m、电荷量为e,其重力不计。
(1)求电子离开偏转电场时的位置到OO'的最小距离和最大距离;
(2)要使所有电子都能垂直打在荧光屏上,
①求匀强磁场的水平宽度L;
②求垂直打在荧光屏上的电子束的宽度
正确答案
见解析。
解析
(1)由题意可知,从0、2t0、4t0……等时刻进入偏转电场的电子离开偏转电场时的位置到OO'的距离最大,在这种情况下,电子的最大距离为
从t0、3t0……等时刻进入偏转电场的电子离开偏转电场时的位置到OO'的距离最小,在这种情况下,电子的最小距离为

(2)①设电子从偏转电场中射出时的偏向角为 ,由于电子要垂直打在荧光屏上,所以电子在磁场中运动半径应为:
设电子离开偏转电场时的速度为vt,垂直偏转极板的速度为vy,则电子离开偏转电场时的偏向角为:

又
解得:
②由于各个时刻从偏转电场中射出的电子的速度大小相等,方向相同,因此电子进入磁场后做圆周运动的半径也相同,都能垂直打在荧光屏上。
由第(1)问知电子离开偏转电场时的位置到OO'的最大距离和最小距离的差值为:

所以垂直打在荧光屏上的电子束的宽度为:
知识点
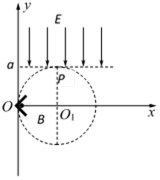
如图所示,在竖直平面内放置一长为L的薄壁玻璃管,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带电荷量为-q、质量为m。玻璃管右边的空间存在着匀强电场与匀强磁场的复合场。匀强磁场方向垂直于纸面向外,磁感应强度为B;匀强电场方向竖直向下,电场强度大小为
求:
(1)小球从玻璃管b端滑出时速度的大小;
(2)从玻璃管进入磁场至小球从b端滑出的过程中,外力F随时间t变化的关系;
(3)通过计算画出小球离开玻璃管后的运动轨迹。
正确答案
见解析。
解析
(1)由

所以小球在管中运动的加速度为 
设小球运动至b端时竖直方向的速度分量为

联立解得小球运动至b端时速度大小为
(2)由平衡条件可知,玻璃管受到的水平外力为

解得外力随时间变化关系为
(3)设小球在管中运动时间为t,小球在磁场中做圆周运动的半径为R,轨迹如图甲所示。t时间内玻璃管的运动距离x = v0t
由牛顿第二定律得
由几何关系得 
所以
可得 sinα=0,故α=0o,
即小球飞离磁场时速度方向垂直于磁场边界向左,小球运动轨迹如图乙所示。
知识点
如图所示,在xoy直角坐标系中,第Ⅰ象限内分布着方向垂直纸面向里的匀强磁场,第Ⅱ象限内分布着方向沿y轴负方向的匀强电场。初速度为零、带电荷量为q、质量为m的离子(不计重力)经过电压为U的电场加速后,从x上的A点垂直x轴进入磁场区域,经磁场偏转后过y轴上的P点且垂直y轴进入电场区域,在电场偏转并击中x轴上的C点。已知OA=OC=d。
求:
(1)离子进入磁场时的速度大小;
(2)电场强度E和磁感应强度B的大小。
正确答案
见解析。
解析
(1)设离子经电压为U的电场加速后获得速度为v,由


(2)离子进入磁场后,洛仑兹力提供向心力,由牛顿第二定律:

依题意可知:r=d
解得:
离子在电场中偏转,做类平抛运动,设经时间t从P点到达C点,由


解得:
知识点
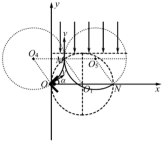
如图所示,在坐标系xOy所在平面内有一半径为a的圆形区域,圆心坐标O1(a , 0),圆内分布有垂直xOy平面的匀强磁场。在坐标原点O处有一个放射源,放射源开口的张角为90°,x轴为它的角平分线。带电粒子可以从放射源开口处在纸面内朝各个方向射出,其速率v、质量m、电荷量+q均相同。其中沿x轴正方向射出的粒子恰好从O1点的正上方的P点射出。不计带电粒子的重力,且不计带电粒子间的相互作用。
(1)求圆形区域内磁感应强度的大小和方向;
(2)a,判断沿什么方向射入磁场的带电粒子运动的时间最长,并求最长时间;
b,若在y≥a的区域内加一沿y轴负方向的匀强电场,放射源射出的所有带电粒子运动过程中将在某一点会聚,若在该点放一回收器可将放射源射出的带电粒子全部收回,分析并说明回收器所放的位置。
正确答案
见解析。
解析
(1)设圆形磁场区域内的磁感应强度为B,带电粒子在磁场中所受的洛伦兹力提供向心力:
其中R=a
则:
由左手定则判断磁场方向垂直于xOy平面向里
(2)沿与x轴45°向下射出的带电粒子在磁场中运动的时间最长,轨迹如图,根据几何关系粒子离开磁场时速度方向沿y轴正方向,∠OO3Q=135º。
设该带电粒子在磁场中运动的时间为t,根据圆周运动周期公式得:
所以: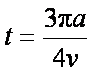
(3)设某带电粒子从放射源射出,速度方向与x轴的夹角为α,做速度v的垂线,截取OO4=a,以O4为圆心a为半径做圆交磁场边界于M点。由于圆形磁场的半径与带电粒子在磁场中运动的半径均为a,故OO1MO4构成一个菱形,所以O4M与x轴平行,因此从放射源中射出的所有带电粒子均沿y轴正方向射出。带电粒子在匀强电场中做匀减速直线运动,返回磁场时的速度与离开磁场时的速度大小相等方向相反,再进入磁场做圆周运动,圆心为O5,OO4O5N构成一平行四边形,所以粒子在磁场中两次转过的圆心角之和为180°,第二次离开磁场时都经过N点。故收集器应放在N点,N点坐标为(2a,0)。
知识点
如图所示,直角坐标系Oxy位于竖直平面内,x轴与绝缘的水平面重合,在y轴右方有垂直纸面向里的匀强磁场和竖直向上的匀强电场,质量为m2=8×10-3kg的不带电小物块静止在原点O,A点距O点l=0.045m,质量m1=1×10-3kg的带电小物块以初速度v0=0.5m/s从A点水平向右运动,在O点与m2发生正碰并把部分电量转移到m2上,碰撞后m2的速度为0.1m/s,此后不再考虑m1、m2间的库仑力,已知电场强度E=40N/C,小物块m1与水平面的动摩擦因数为μ=0.1,取g=10m/s2,求:
(1)碰后m1的速度;
(2)若碰后m2做匀速圆周运动且恰好通过P点,OP与x轴的夹角θ=30°,OP长为lop=0.4m,求磁感应强度B的大小;
(3)其它条件不变,若改变磁场磁感应强度的大小为B/使m2能与m1再次相碰,求B/的大小?
正确答案
见解析。
解析
(1)m1与m2碰前速度为v1,由动能定理

代入数据解得:
设v2=0.1m/s,m1、m2正碰,由动量守恒有:
代入数据得:
(2)m2恰好做匀速圆周运动,所以
得:q=2×10-3C(1分)
粒子受洛仑兹力提供向心力,设圆周的半径为R则

轨迹如图,由几何关系有:
解得:B=1T(1分)
(3)当m2经过y轴时速度水平向左,离开电场后做平抛运动,m1碰后做匀减速运动。
m1匀减速运动至停,其平均速度为:
由牛顿第二定律有:
m1停止后离O点距离:
则m2平抛的时间:
平抛的高度:
设m2做匀速圆周运动的半径为R/,由几何关系有:
由
联立得:
知识点
如图,竖直平面








(1)小球运动到
(2)悬线断裂前瞬间拉力的大小;
(3)
正确答案
见解析。
解析
1)小球从A运到O的过程中,根据动能定理:

则得小球在

(2)小球运到


由③、④得:

(3)绳断后,小球做匀变速曲线运动,可分解为水平方向匀变速和竖直方向自由落体运动。
所以,小球水平方向加速度大小为:

小球从


竖直方向

知识点
质谱仪的工作原理示意图如右图所示,带电粒子被加速电场加速后,进人速度选择器,速度选择器内相互正交的匀强磁场和匀强电场的强度分别为B 和E,平板S 上有可让粒子通过的狭缝P 和记录粒子位置的胶片A1A2,平板S下方有强度为B0的匀强磁场,下列表述正确的是
正确答案
解析
略
知识点
法拉第曾提出一种利用河流发电的设想,并进行了实验研究。实验装置的示意图如图所示,两块面积均为S的矩形金属板,平行、正对、竖直地全部浸在河水中,间距为d。水流速度处处相同,大小为v,方向水平,金属板与水流方向平行。地磁场磁感应强度的竖直分量为B,水的电阻率为ρ,水面上方有一阻值为R的电阻通过绝缘导线和电键K连接到两个金属板上,忽略边缘效应。则电阻R消耗的电功率( )
正确答案
解析
略
知识点
如图所示,是一种电子扩束装置的原理示意图。直角坐标系原点O处有一电子发生器,朝xOy平面内x≥0区域任意方向发射电子,电子的速率均为v0,已知电子的电荷量为e、质量为m。在0≤x≤d的区域内分布着沿x轴负方向的匀强电场,场强大小

(1)求电子进入磁场时速度的大小。
(2)当感光板ab沿x轴方向平移到某一位置时,恰好没有电子打到板上,求感光板到y轴的距离x1。
(3)保持 (2)中感光板位置不动,若使所有电子恰好都能打到感光板上,求磁感应强度的大小以及电子打到板上形成亮线的长度。
正确答案
(1)
(2)
(3)L=
解析
(1)根据动能定理:
得
(2)由v0=知,对于沿y轴负方向射出的电子进入磁场时与边界线夹角θ=60°
若此电子不能打到ab板上,则所有电子均不能打到ab板上。
当此电子轨迹与ab板相切时,根据洛伦兹力提供向心力有
又
得
由几何知识
解得
(3)易知沿y轴正方向射出的电子若能打到ab板上,则所有电子均能打到板上。其临界情况就是此电子轨迹恰好与ab板相切
此时
故
由
解得
此时,所有粒子恰好都能打到板上
电子在电场中运动过程
沿y轴方向的位移
电子在磁场中运动过程,沿y轴负方向的偏转量
沿y轴正方向的偏转量
电子打到板上形成亮线的长度
知识点
如图所示,匀强电场区域和匀强磁场区域是紧邻的且宽度相等均为d,电场方向在纸面内竖直向下,而磁场方向垂直纸面向里。一质量为m,电量为q的正电粒子 (重力不计) ,从O点以速度ν0沿垂直电场方向进入电场,从A点射出电场进入磁场,离开电场时带电粒子在电场方向的偏转位移为电场宽度的一半,粒子从磁场右边界上C点水平穿出,求:
(1)粒子进入磁场时的速度ν为多少?
(2)电场强度E和磁感应强度B的大小。
正确答案
见解析。
解析
(1)粒子在电场偏转
垂直电场方向
平行电场方向
解得Vy=V0
到达A点的速度为
进入磁场时速度方向与水平方向成θ
(2)在电场中Vy=at 
解得
在磁场中粒子做匀速圆周运动,如图所示,由图得圆周运动半径
又
得
知识点
在如图所示的直角坐标系中,对于第I象限和第IV象限,其中一个象限有垂直纸面向外的匀强磁场B,另一象限有平行纸面的匀强电场E,一个比荷为


(1)问电荷带正电还是带负电,匀强电场存在哪个象限,方向如何?
(2)求磁感应强度和电场强度的大小;
(3)求电荷第三次经过x轴的位置。
(4)若电荷第三次经过x轴时突然改变匀强电场的大小,使电荷第四次回到x轴时恰好是P点,求改变后的电场强度大小。
正确答案
(1)负电,匀强电场在第I象限,方向与X轴成450
(2)
(3)x=
(4)
解析
(1)负电,匀强电场在第I象限,方向与X轴成450
(2)在第四象限中,由向心力公式得:


在电场中, 

解得:
(3)由图可知:
(4)第三次经过x轴后,电荷做类平抛运动,如图所示,

由牛顿第二定律:
解得:
知识点
如图所示,质量为m、电荷量为+q的粒子从坐标原点O以初速度v0射出,粒子恰好经过A点,O、A两点长度为l ,连线与坐标轴+y方向的夹角为
(1)若在平行于x轴正方向的匀强电场E1中,粒子沿+y方向从O点射出,恰好经过A点;若在平行于y轴正方向的匀强电场E2中,粒子沿+x方向从O点射出,也恰好能经过A点,求这两种情况电场强度的比值
(2)若在y轴左侧空间(第Ⅱ、Ⅲ象限)存在垂直纸面的匀强磁场,粒子从坐标原点O,沿与+y轴成300 的方向射入第二象限,恰好经过A点,求磁感应强度B。
正确答案
(1)
(2)
解析
(1)在电场E1中


在电场E2中


联立①②③④得
(2)设轨迹半径为R,轨迹如图所示,

由几何知识可得

解得
又由
得
由③⑤得
知识点
扫码查看完整答案与解析