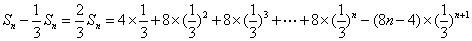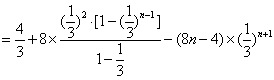- 由递推关系式求数列的通项公式
- 共97题
数列





(1)求数列
(2)若




正确答案
见解析。
解析
(1)
知识点
正确答案
见解析。
解析
知识点
已知:数列
(1)求数列
(2)若

正确答案
见解析。
解析
(1)n=1时,



(i)-(ii)得 
又
(2)
知识点
设数列


(1)求数列
(2)设



正确答案
见解析。
解析
(1)因为

所以当

当

①-②得,
所以
因为
所以
(2)由(1)得
所以

所以

知识点
已知函数
(1)求a的取值范围;
(2)令

正确答案
见解析。
解析
知识点
已知数列



(1)当

(2)当

(3)问:使

正确答案
见解析
解析
(1)当




(2) 















因为

(3)假设存在常数
















从而


知识点
在数列


(1)求数列
(2)求证:数列
(3)设数列



正确答案
见解析。
解析
(1)



∴
(2)
∴
∴
∴数列


(3)由(1)知,
∴
∴
……………………………10分

知识点
已知数列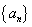
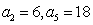
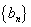
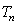
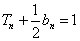
(1)求数列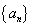
(2) 求证:数列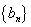
(3) 记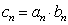
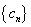
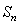
正确答案
见解析。
解析
(1)设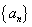
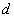
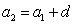
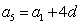
∵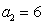
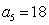
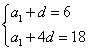
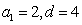
∴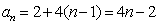
(2)当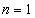
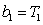
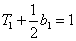
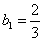
当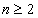
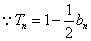
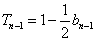
∴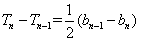
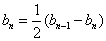
∴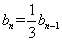
∴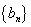
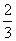
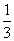
(3)由(2)可知: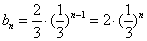
∴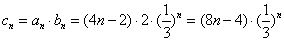
∴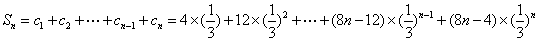
∴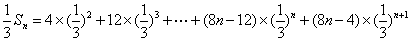
∴
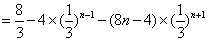
∴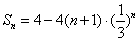
知识点
已知



(1)求数列{an}和数列{bn}的通项公式;
(2)将数列{bn}中的第a1项,第a2项,第a3项,……,第an项,……删去后剩余的项按从小到大的顺序排成新数列(cn},求数列{cn}的前2013项的和。
正确答案
见解析。
解析
知识点
等差数列







(1)求

(2)记




正确答案
见解析。
解析
(1)由已知可得
解直得,


(2)由(1)得,
由已知得 

①-②得

知识点
扫码查看完整答案与解析