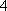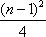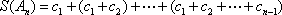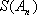- 由递推关系式求数列的通项公式
- 共97题
已知数列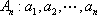
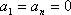
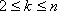
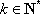
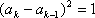
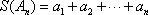
(1)写出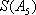
(2)求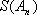
正确答案
(1)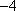
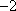

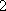
(2)
解析
(1)由题设,满足条件的数列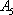
1)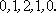
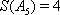
2)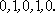
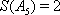
3)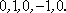
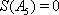
4)
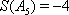
5)
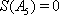
6)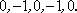
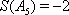
所以,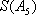
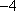
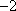

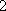
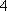
(2)由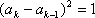
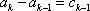
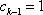
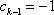
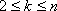
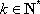
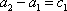

…
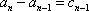
所以
因为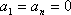



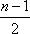
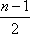
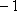
所以

则当
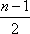
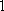
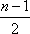
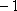
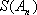
此时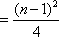
证明如下:
假设
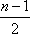

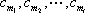
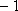



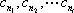
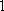

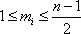
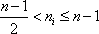
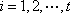
所以
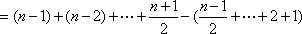
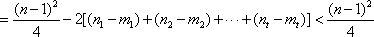
所以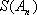
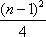
知识点
已知数列



(1)求证:任何的等差数列不可能是“Z数列”;
(2)若正数列




(3)若数列

正确答案
见解析
解析
解析:(1)设等差数列



所以任何的等差数列不可能是“Z数列” 4分
或者根据等差数列的性质:
所以任何的等差数列不可能是“Z数列” 4分
(2)假设




等比数列


其他的也可以:
等比数列



补充说明:分析:
根据几何意义只要
(3)因为




同理:

因为数列
所以

知识点
已知数列





(1)求

(2)记数列




正确答案
见解析。
解析
(1)因为



又
得

(2)因为
而

知识点
定义数列





(1)设





(2)设数列




(3)设数列






正确答案
见解析
解析
解析:假设数列

即存在常数


不妨取




所以数列

而数列


由


所以数列

(2)证明:由数列


即存在常数


即有
则
所以
同理
所以
因此对任意的

(3)解:当
当
综上,
即存在


所以数列

当



当



综上
所以数列



知识点
已知数列
(1)试证数列

(2)在数列
(3)试证在数列


正确答案
见解析
解析
(1) 证明:由an+an+1=2n,得an+1=2n-an,
所以
又因为


所以an-


(2) 假设在数列{bn}中,存在连续三项bk-1,bk,bk+1(k∈N*, k≥2)成等差数列,则bk-1+bk+1=2bk,即[2k-1-(-1)k-1]+[2k+1-(-1)k+1]=2[2k-(-1)k],即2k-1=4(-1)k-1。
① 若k为偶数,则2k-1>0,4(-1)k-1=-4<0,所以,不存在偶数k,使得bk-1,bk,bk+1成等差数列,(7分)
② 若k为奇数,则当k≥3时,2k-1≥4,而4(-1)k-1=4,所以,当且仅当k=3时,bk-1,bk,bk+1成等差数列。
综上所述,在数列{bn}中,有且仅有连续三项b2,b3,b4成等差数列,(9分)
(3) 要使b1,br,bs成等差数列,只需b1+bs=2br,
即3+2s-(-1)s=2[2r-(-1)r],即2s-2r+1=(-1)s-2(-1)r-3,(﹡) (10分)
① 若s=r+1,在(﹡)式中,左端2s-2r+1=0,
右端(-1)s-2(-1)r-3=(-1)s+2(-1)s-3=3(-1)s-3,
要使(﹡)式成立,当且仅当s为偶数时,又s>r>1,且s,r为正整数,
所以当s为不小于4的正偶数,且s=r+1时,b1,br,bs成等差数列,(12分)
② 若s≥r+2时,在(﹡)式中,左端2s-2r+1≥2r+2-2r+1=2r+1,
由(2)可知,r≥3,所以r+1≥4,所以左端2s-2r+1≥16(当且仅当s为偶数、r为奇数时取“=”);右端(-1)s-2(-1)s-3≤0.所以当s≥r+2时,b1,br,bs不成等差数列,
综上所述,存在不小于4的正偶数s,且s=r+1,使得b1,br,bs成等差数列。
知识点
已知数列


(1)求数列{
(2)若


(3)根据笛卡尔符号法则,有:若关于实数



正确答案
见解析。
解析
知识点
已知数列
(1)求数列
(2)若


正确答案
见解析。
解析
(1)


(1)-(2)得
又
(2)
知识点
在数列

(1)求数列
(2)求证:数列
(3)设数列



正确答案
见解析。
解析
(1)∵
∴数列{


∴
(2)∵
∴
∴
∴数列


(3)由(1)知,


∴
∴
于是
…………………………………………………………………………………………… 9分
两式①-②相减得
=
∴ 
知识点
设





正确答案
解析
略
知识点
设数列




(1)求数列
(2)求数列


正确答案
(1)

解析
(1)


∴
∴数列

(2)


知识点
扫码查看完整答案与解析