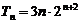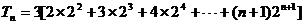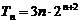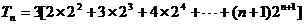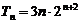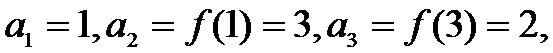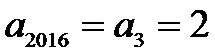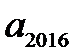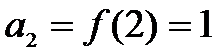- 由递推关系式求数列的通项公式
- 共97题
19. 已知数列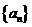
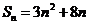
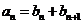
(I)求数列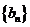
(II)令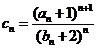
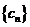
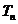
正确答案
(Ⅰ)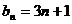
解析
试题分析:(Ⅰ)由题意得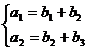
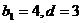
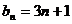
(Ⅱ)由(Ⅰ)知
利用“错位相减法”即得
试题解析:(Ⅰ)由题意当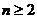
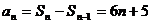
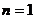
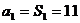
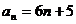
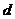
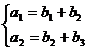
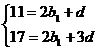

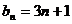
(Ⅱ)由(Ⅰ)知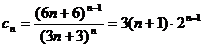
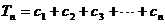
,所以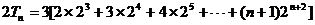
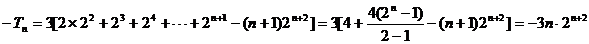
所以
考查方向
知识点
23. 已知数列


(1)若


(2)设




(3)设




正确答案
(1)
(2)见解析
(3)
解析
(1)由

故
所以
(2)由
得



因为
所以

故

(3)因为

当
=
当


因为



特别地

此时对任意

当


由指数函数的单调性知,


最小值为
由题意,


由

解得
综上所述,

知识点
5.已知函数f (x) 的部分对应值如表所示. 数列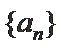
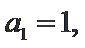


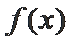
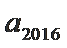
正确答案
解析
根据表格可以得到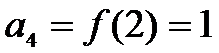
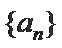
考查方向
解题思路
根据表格逐步求出数列的前几项,看数列什么时候开始循环,得到数列 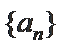
易错点
看不懂表格的意思,不能得到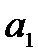
知识点
16.数列{an}的前n项和为Sn,若Sn-Sn一1=2n-l (
正确答案
5
解析
由条件Sn-Sn一1=2n-l (
当n=3时,S3-S2=2×3-1=5,即a3=5
所以a1+a3=5
考查方向
解题思路
本题考查数列递推式,解题步骤如下:
根据条件求出S1= a1=0;2. 再根据S3-S2=a3求出a3.即可得到答案
易错点
对递推式不熟悉,代入的时候出错。
知识点
4. 已知数列


正确答案
解析
当

考查方向
本题主要考查了数列中已知求;
解题思路
先求出
易错点
本题易在计算上出现错误,特别是
知识点
扫码查看完整答案与解析