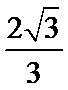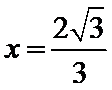热门试卷

X 查看更多试卷

题型：简答题

简答题 · 16 分

18.如图，在平面直角坐标系中，已知以为圆心的圆：
及其上一点．
⑴ 设圆与轴相切，与圆外切，且圆心在直线上，求圆的标准方程；
⑵ 设平行于的直线与圆相交于两点，且，求直线的方程；
⑶ 设点满足：存在圆上的两点和，使得，求实数的取值范围．

正确答案

（1）因为在直线上，设，因为与轴相切，
则圆为，
又圆与圆外切，圆：，
则，解得，即圆的标准方程为；

⑵ 由题意得，设，则圆心到直线的距离,
则，，即，
解得或，即：或；

⑶ ，即，即，
，
又,
即，解得，
对于任意，欲使，
此时，只需要作直线的平行线，使圆心到直线的距离为，
必然与圆交于两点，此时，即，
因此对于任意，均满足题意，
综上．

知识点

两圆的公切线条数及方程的确定

题型：单选题

单选题 · 5 分

8．直线3x+4y=b与圆相切，则b=（）

A-2或12

B2或-12

C-2或-12

D2或12

正确答案

解析

∵直线与圆心为（1,1）,半径为1的圆相切，∴＝1或12,故选D.

考查方向

本题主要考查利用圆的一般方程求圆的圆心和半径，直线与圆的位置关系，以及点到直线的距离公式的应用.

解题思路

先确定圆的圆形，然后用点到直线的距离公式求解

易错点

圆的一般方程转换成标准方程换错，点到直线的距离求错

知识点

两圆的公切线条数及方程的确定

题型：填空题

填空题 · 5 分

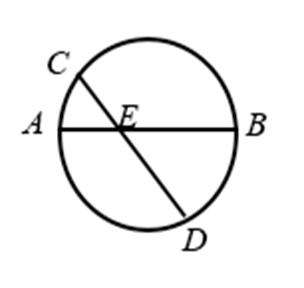
13.如图，AB是圆的直径，弦CD与AB相交于点E，BE=2AE=2，BD=ED，则线段CE的长为__________.

正确答案

解析

试题分析：设，则由相交弦定理得，，又，所以，因为是直径，则，，在圆中，则，即，解得

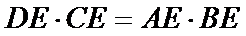
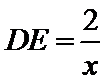
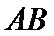
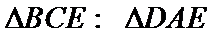
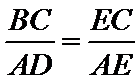
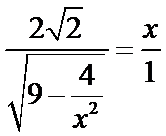
考查方向

本题考查了相交弦定理等知识点。

解题思路

应用相交弦定理、切割线定理要抓住几个关键内容：如线段成比例与相似三角形、圆的切线及其性质、与圆有关的相似三角形等．本题根据相交弦定理即可求出CE长。

易错点

对相关定理不熟悉导致本题失分。

知识点

两圆的公切线条数及方程的确定

题型：单选题

单选题 · 5 分

2．复数=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 圆系方程

百度题库 > 高考 > 文科数学 > 两圆的公切线条数及方程的确定

扫码查看完整答案与解析