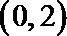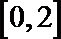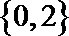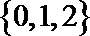· 不等式的解法

· 一元二次不等式的解法

一元二次不等式的解法
共209题

· 不等式的解法

· 一元二次不等式的解法

一元二次不等式的解法
共209题

热门试卷

X 查看更多试卷

1

题型：简答题

|

简答题 · 12 分

20．已知分别在射线（不含端点）上运动，，在中，角、、所对的边分别是、、．

（Ⅰ）若、、依次成等差数列，且公差为2．求的值；

（Ⅱ）若，，试用表示的周长，

并求周长的最大值．

正确答案

（Ⅰ）、、成等差，且公差为2，

、. 又，，

，，

恒等变形得，解得或.又，.

（Ⅱ）在中，，，，.

的周长

，

又，,

当即时，取得最大值．

解析

解析已在路上飞奔，马上就到！

知识点

一元二次不等式的解法

1

题型：填空题

|

填空题 · 4 分

17．已知函数，若互不相同，且，则的取值范围是_______

正确答案

(10,12)

解析

解析已在路上飞奔，马上就到！

知识点

一元二次不等式的解法

1

题型：单选题

|

单选题 · 5 分

1．已知集合，，则( )

A

B

C

D

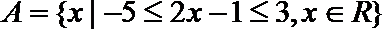
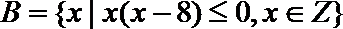
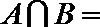
正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

交集及其运算一元二次不等式的解法

1

题型：简答题

|

简答题 · 14 分

18．已知集合A=，集合B=

（1）若，求实数m的值；

（2）若，求实数m的取值范围。

正确答案

解：由已知得：集合A=，集合B=

（1）因为，所以所以，所以m=2；

（2）

因为，所以或，

所以或

解析

解析已在路上飞奔，马上就到！

知识点

子集与真子集交集及其运算补集及其运算一元二次不等式的解法

1

题型：简答题

|

简答题 · 14 分

20．在中，角的对边分别为，且．

（1）求的值；

（2）若，求面积的最大值．

正确答案

（1）因为，所以．

又

=+=．

（2）由已知得，

因为，所以．

又因为，

所以，当且仅当时，取得最大值．

此时．

所以的面积的最大值为．

解析

解析已在路上飞奔，马上就到！

知识点

一元二次不等式的解法

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 一元二次不等式的解法

扫码查看完整答案与解析