· 不等式的解法

· 一元二次不等式的解法

一元二次不等式的解法
共209题

· 不等式的解法

· 一元二次不等式的解法

一元二次不等式的解法
共209题

热门试卷

X 查看更多试卷

1

题型：简答题

|

简答题 · 14 分

20．已知函数

（1）若不等式的解集为或,求的表达式;

（2）在（1）的条件下, 当时, 是单调函数, 求实数k的取值范围;

（3）设, 且为偶函数, 判断＋能否大于零?

正确答案

（1）由已知不等式的解集为或，故且方程的两根为，由韦达定理，得解得因此，

（2）则

,

当或时, 即或时, 是单调函数.

（3） ∵是偶函数∴,

∵设则.又 ∴

＋ ,

∴＋能大于零.

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质函数奇偶性的性质一元二次不等式的解法

1

题型：单选题

|

单选题 · 5 分

11. 实数，满足，则的取值范围是（）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

一元二次不等式的解法

1

题型：单选题

|

单选题 · 5 分

2．设集合,，则等于（）

A

B

C

D

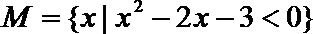
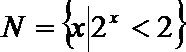
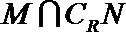
正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

交、并、补集的混合运算一元二次不等式的解法

1

题型：单选题

|

单选题 · 5 分

1．已知集合，则集合等于（）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

一元二次不等式的解法

1

题型：填空题

|

填空题 · 5 分

13．已知向量满足，，则的夹角为．

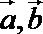
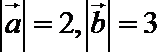
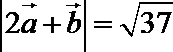
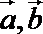
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

一元二次不等式的解法

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 一元二次不等式的解法

扫码查看完整答案与解析